Übung Aufgaben 6 (WS 24 25): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „==Aufgabe 6.1== Geben Sie eine formal korrekte Definition für die Halbgerade <math>\ AB^-</math> an, ohne die Zwischenrelation zu verwenden. Lösung von Au…“) |
|||
| Zeile 2: | Zeile 2: | ||
Geben Sie eine formal korrekte Definition für die Halbgerade <math>\ AB^-</math> an, ohne die Zwischenrelation zu verwenden. | Geben Sie eine formal korrekte Definition für die Halbgerade <math>\ AB^-</math> an, ohne die Zwischenrelation zu verwenden. | ||
| − | [[Lösung von Aufg. 6.1P ( | + | [[Lösung von Aufg. 6.1P (WS_24_25)]] |
==Aufgabe 6.2== | ==Aufgabe 6.2== | ||
| Zeile 8: | Zeile 8: | ||
'''''M'' ist konvex, wenn gilt: ...''' | '''''M'' ist konvex, wenn gilt: ...''' | ||
| − | [[Lösung von Aufg. 6.2P ( | + | [[Lösung von Aufg. 6.2P (WS_24_25)]] |
== Aufgabe 6.3 == | == Aufgabe 6.3 == | ||
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. | Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex. | ||
| − | [[Lösung von Aufg. 6.3P ( | + | [[Lösung von Aufg. 6.3P (WS_24_25)]] |
== Aufgabe 6.4 == | == Aufgabe 6.4 == | ||
| Zeile 19: | Zeile 19: | ||
b) Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 6.3 nicht wahr ist. | b) Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 6.3 nicht wahr ist. | ||
| − | [[Lösung von Aufg. 6.4P ( | + | [[Lösung von Aufg. 6.4P (WS_24_25)]] |
== Aufgabe 6.5 == | == Aufgabe 6.5 == | ||
Beweisen Sie den Satz von Pasch.<br /> | Beweisen Sie den Satz von Pasch.<br /> | ||
| − | [[Lösung von Aufg. 6.5P ( | + | [[Lösung von Aufg. 6.5P (WS_24_25)]] |
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 9. Oktober 2024, 14:46 Uhr
Inhaltsverzeichnis |
Aufgabe 6.1
Geben Sie eine formal korrekte Definition für die Halbgerade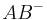 
an, ohne die Zwischenrelation zu verwenden.
Lösung von Aufg. 6.1P (WS_24_25)
Aufgabe 6.2
Definieren Sie den Begriff: "konvexe Punktmenge" indem Sie die verbal formulierte Definition (siehe Wiki-Skript) in eine geeignete "Mengenschreibweise" übersetzen.
M ist konvex, wenn gilt: ...
Lösung von Aufg. 6.2P (WS_24_25)
Aufgabe 6.3
Beweisen Sie: Der Durchschnitt zweier konvexer Punktmengen ist konvex.
Lösung von Aufg. 6.3P (WS_24_25)
Aufgabe 6.4
a) Formulieren Sie die Kontraposition der Implikation aus Aufgabe 6.3.
b) Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 6.3 nicht wahr ist.
Lösung von Aufg. 6.4P (WS_24_25)
Aufgabe 6.5
Beweisen Sie den Satz von Pasch.
