Lösung von Aufgabe 1.2 WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 10: | Zeile 10: | ||
<math>\ |AB| + |BC| = |AC|</math> | <math>\ |AB| + |BC| = |AC|</math> | ||
| + | |||
| + | entsprechend (**) haben wir zu zeigen, dass <math>\ |A'B'| + |B'C'| = |A'C'|</math> gilt. | ||
Version vom 19. Oktober 2010, 16:42 Uhr
Es seien  drei paarweise verschiedene Punkte mit
drei paarweise verschiedene Punkte mit
(*) 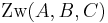 .
.
zu zeigen:
(**) 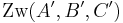
Wir übersetzen zunächst (*):
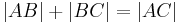
entsprechend (**) haben wir zu zeigen, dass 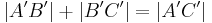 gilt.
gilt.

