Fixpunkt, Fixgerade, Fixpunktgerade (2010): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Definition 3.1: (Fixpunkt einer Abbildung \phi) |
*m.g.* (Diskussion | Beiträge) (→Definition des Begriffs Fixpunkt einer Abbildung) |
||
| Zeile 17: | Zeile 17: | ||
=== Definition des Begriffs Fixpunkt einer Abbildung === | === Definition des Begriffs Fixpunkt einer Abbildung === | ||
| − | ===== Definition 3.1: (Fixpunkt einer Abbildung <math>\phi</math> )===== | + | ===== Definition 3.1: (Fixpunkt einer Abbildung <math>\ \phi</math> )===== |
| − | ::Ein Punkt <math>\ F</math> heißt Fixpunkt einer Abbildung <math>\phi</math>, wenn ... . | + | ::Ein Punkt <math>\ F</math> heißt Fixpunkt einer Abbildung <math>\ \phi</math>, wenn ... . |
Version vom 1. November 2010, 18:36 Uhr
Inhaltsverzeichnis |
Begriff des Fixpunktes
Beispiele/Gegenbeispiele
Definition des Begriffs Fixpunkt einer Abbildung
Definition 3.1: (Fixpunkt einer Abbildung  )
)
- Ein Punkt
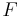 heißt Fixpunkt einer Abbildung
heißt Fixpunkt einer Abbildung  , wenn ... .
, wenn ... .
- Ein Punkt

