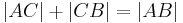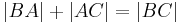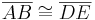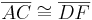Benutzer:*m.g.*: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Axiome) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 74: | Zeile 74: | ||
==== Euklidisches Parallelenaxiom ==== | ==== Euklidisches Parallelenaxiom ==== | ||
::Zu jedem Punkt <math>\ P</math> außerhalb einer Geraden <math>\ g</math> gibt es höchstens eine Gerade <math>\ h</math>, die durch <math>\ P</math> geht und zu <math>\ g</math> parallel ist. | ::Zu jedem Punkt <math>\ P</math> außerhalb einer Geraden <math>\ g</math> gibt es höchstens eine Gerade <math>\ h</math>, die durch <math>\ P</math> geht und zu <math>\ g</math> parallel ist. | ||
| + | |||
| + | |||
| + | <ggb_applet width="645" height="623" version="3.2" ggbBase64="UEsDBBQACAAIAHFVZD0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vjdcus0EL7mPIXGF9zVteSfOEPSM2m5oDOBwuRwmOFOthVHVLaMLadJXoaH4cVYSXb+2pMmLQMMvXG1u17tfvvtSs7o46oQaMnqhsty7GDXcxArU5nxMh87rZpfxc7Hmw+jnMmcJTVFc1kXVI0d3yWOlrf85sNXo2YhnxAVxuQzZ09jZ05FwxzUVDWjWbNgTB3IabvigtN6/ZD8xlLV7BTWyX1ZtbCLqluQpUU25U2/vDYbVoKrb/mSZ6xGQqZjJwohdPjvM6sVT6kYO4FnJWTskCMliHytXciab2SptPnO+RwkCDV8wwARomWja5PoiLWp4BmnpU7GxAFGCD3xTC0ghCAEl4znC4g1xAPrLZWyzmbrRrECrX5ltRw7Vz4xSK/tEgeeXjUQGOwYmsV6f2X8sOWMKQV1aRBdsR1iec2zg8V9cyvFTlRJXqo7Wqm2NkX1O9FMrfUGsFetI56UuWCdjADmC5Y+JnI1syj41vWndWVeMQEl+Z0Uska1xhcyz7tnYp/GRke6tfKMjWcsOh/a6VaPh8RYmGdin8ZK8NKG1mWO+6yx12/DG6QFGkbg4jZ5QRMGtXVQW3I17RfAgccuVWxf+KEtEmiCfRZsfeK/y+fo+og/o0dWl0xYlpRQ21a2DVpqNtq9TCAZS3kBS6voIKG6XD9DAFaasbxmfeC2hSxgRuvtM/FIPLrug9AxNBBrqmAWQD5K5zKrOMuZaMtcN62Chhk7hZu7DsqoAr2jHT/J+tH0+Ce2UogmcgkaSFGgWUX//AOKyYQG8DsqhES/MKHMzkywgkGrKcMqQ8otuj8627kizYjoh0Gn39UJ1C8yzHCRimpBQdI3kaBrGBj7oBh/38vsECpaAuQGB+jbSjvQRa0Yy7ohqbpOQBW4NH21VzEDdINWYyd2feDyGloeQogdtLGvGyvbhXqAmJ39jiIWlFfg+en/AU/gxhYe7EbRZeiksihomaGSFrDTFCaEgYTrgwNRTzMIUayRsjC0qldQ66pz8AxoPWy2OFLncP6oBbR5yZrGDEm1Pw7fUwzv7FI8zOcNUxq7cGiJ1Y/alyu1w/oKu4PAvuK7oQU7cPEwio+H7Ikk2e+ltWnsqOMFHMQpV5dwd/If5u7ZzMXYJR2aoSb826n7UMNUzWVJxQsknlgS02ckTi4gcXIGifGrLN6D4f00PsFTQ871lq8A7FUQux7c5nZ/0TmUxRdy9rAs96WCwxtgOKpI8qWKTE9X5LAHpm/qgSgwYOtHYh8XT42rqAMXn1cNuIO5cUCC/hjzfXfoefGuFLZEOHTJYBC9hf93vE7FMe+nFuXJM5TT0yjDFYanWxTTM4hP/mXinxcdfFSwcgmxybpBaOV1x+zaszuiTS9ZYXvXAB3uRBu8N5tg9NV8hSa9/aS3mhBdxcCNvEHgh77nDwdBANf+id9tMQk0bYgbERJGXoRxhAMfzqBJCGG6BMfDeEAGYRDHZDh4ufNgyqZ8ztO3dV5qOZE848RtR5avaSWbby5pw9tX2vALpX9zH55qtHccKCdP2w6Vf3TenMozcD0vxAQT4hMSD7oLoOeGEfFIGARDj/iBN8CXQXC9//FiPti7Xyxu/gJQSwcIaVCnm7IEAADjEAAAUEsBAhQAFAAIAAgAcVVkPWlQp5uyBAAA4xAAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAADsBAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" /> | ||
Version vom 4. November 2010, 11:17 Uhr
Axiome von Moise/Downs
- Inzidenzaxiome:
Axiom I.0:
- Geraden und Ebenen sind Punktmengen.
Axiom I.1: (Axiom von der Geraden)
- Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
Axiom I.2:
- Zu jeder Geraden gibt es wenigstens zwei Punkte, die dieser Geraden angehören.
Axiom I.3:
- Es gibt wenigstens 3 Punkte, die nicht kollinear sind.
Axiom I.4:
- Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. Jede Ebene enthält (wenigstens) einen Punkt.
Axiom I.5:
- Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
Axiom I.6:
- Wenn zwei Ebenen einen Punkt gemeinsam haben, so haben sie noch mindestens einen weiteren Punkt gemeinsam.
Axiom I.7:
- Es gibt vier Punkte, die nicht komplanar sind.
- Abstandsaxiome:
Axiom II.1: (Abstandsaxiom)
- Zu je zwei Punkten
 und
und  gibt es eine eindeutig bestimmte nicht negative reelle Zahl
gibt es eine eindeutig bestimmte nicht negative reelle Zahl 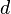 mit
mit 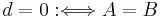 .
.
Axiom II.2:
- Für zwei beliebige Punkte
 und
und  gilt
gilt 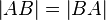 .
.
Axiom II/3: (Dreiecksungleichung)
- Für drei beliebige Punkte
 und
und  gilt:
gilt: 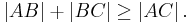
- Falls
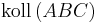 , dann ist eine der folgenden Gleichungen erfüllt:
, dann ist eine der folgenden Gleichungen erfüllt:
- Ist umgekehrt eine dieser drei Gleichungen erfüllt, so sind
 ,
,  und
und  kollinear.
kollinear.
Axiom III.1: (Axiom vom Lineal)
- Zu jeder nicht negativen reelen Zahl
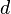 gibt es auf jedem Strahl
gibt es auf jedem Strahl  genau einen Punkt, der zum Anfangspunkt von
genau einen Punkt, der zum Anfangspunkt von  den Abstand
den Abstand 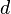 hat.
hat.
Axiom III.2: (Das Axiom von Pasch)
- Gegeben sei ein Dreieck
 . Ferner sei
. Ferner sei  eine Gerade, die durch keinen der drei Eckpunkte
eine Gerade, die durch keinen der drei Eckpunkte  geht. Wenn
geht. Wenn  eine der drei Seiten des Dreiecks
eine der drei Seiten des Dreiecks  schneidet, dann schneidet
schneidet, dann schneidet  genau eine weitere Seite des Dreiecks
genau eine weitere Seite des Dreiecks  .
.
Axiom IV.1: (Winkelmaßaxiom)
- Zu jedem Winkel
 gibt es genau eine reelle Zahl
gibt es genau eine reelle Zahl 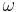 zwischen 0 und 180.
zwischen 0 und 180.
- Zu jedem Winkel
Axiom IV.2: (Winkelkonstruktionsaxiom)
- Es sei
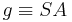 eine Gerade in der Ebene
eine Gerade in der Ebene  . Zu jeder reellen Zahl
. Zu jeder reellen Zahl 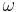 mit
mit 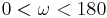 gibt es in jeder der beiden durch
gibt es in jeder der beiden durch  bestimmten Halbebenen der Ebene
bestimmten Halbebenen der Ebene  genau einen Strahl
genau einen Strahl 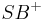 mit
mit 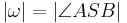
- Es sei
Axiom IV.3: (Winkeladditionsaxiom)
- Wenn der Punkt
 zum Inneren des Winkels
zum Inneren des Winkels  gehört , dann gilt
gehört , dann gilt 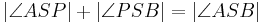 .
.
- Wenn der Punkt
Axiom IV.4: (Supplementaxiom)
- Nebenwinkel sind supplementär.
Axiom V: (Kongruenzaxiom SWS)
- Wenn für zwei Dreiecke
 und
und  die folgenden 3 Kongruenzen
die folgenden 3 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und  kongruent zueinander.
kongruent zueinander.
Euklidisches Parallelenaxiom
- Zu jedem Punkt
 außerhalb einer Geraden
außerhalb einer Geraden  gibt es höchstens eine Gerade
gibt es höchstens eine Gerade  , die durch
, die durch  geht und zu
geht und zu  parallel ist.
parallel ist.
- Zu jedem Punkt