Diskussion:Lösungen zu Tutorium Aufgaben 1: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: Mit der Lösung zu Aufgabe 1 bin ich nicht einverstanden. Betrachten wir die Menge A: alle geraden natürlichen Zahlen lassen sich Ausdrücken als (2n) Betrachten wi...) |
|||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
Eine gerade Zahl quadriert gibt wieder eine gerade Zahl | Eine gerade Zahl quadriert gibt wieder eine gerade Zahl | ||
| − | (2n)^2 = 4n^2 = 2 | + | <math>(2n)^2 = 4n^2 = 2(2n^2)</math> |
| + | |||
Vielfache von Zwei sind immer gerade. | Vielfache von Zwei sind immer gerade. | ||
| − | Also sind alle geraden natürlichen Zahlen in Menge B enthalten. | + | -> Also sind alle geraden natürlichen Zahlen in Menge B enthalten. |
| Zeile 18: | Zeile 19: | ||
eine ungerade natürliche Zahl lässt sich darstellen als (2n-1) | eine ungerade natürliche Zahl lässt sich darstellen als (2n-1) | ||
| − | (2n-1)^2 = 4n^2 - 4n +1 = 2*(2n^2) + 2*(2n) +1 | + | <math>(2n-1)^2 = 4n^2 - 4n +1 = 2*(2n^2) + 2*(2n) +1</math> |
| + | |||
Aus dem letzten Audruck folgt, dass die Zahl ungerade sein muss, denn Vielfache von 2 sind immer gerade und zwei gerade Zahlen addiert sind auch gerade. Addiert man zu einer geraden Zahl 1 so ist sie ungerade. | Aus dem letzten Audruck folgt, dass die Zahl ungerade sein muss, denn Vielfache von 2 sind immer gerade und zwei gerade Zahlen addiert sind auch gerade. Addiert man zu einer geraden Zahl 1 so ist sie ungerade. | ||
| − | Also sind die Mengen A und Mengen B gleich. | + | -> Also sind die Mengen A und Mengen B gleich. |
| + | |||
| + | : Stimmt. --[[Benutzer:Jp1234|Jp1234]] 18:17, 19. Okt. 2010 (UTC) | ||
| + | |||
| + | : Wobei streng genommen auch die Teilmenge stimmt, denn jede Menge ist gleichzeitig Teilmenge von sich selbst und zwei Mengen sind genau dann gleich, wenn jede eine Teilmenge der anderen ist. Nur ist es keine echte Teilmenge.--[[Benutzer:Ridcully1975|Ridcully1975]] 21:52, 19. Okt. 2010 (UTC) | ||
| + | |||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 16. November 2010, 22:04 Uhr
Mit der Lösung zu Aufgabe 1 bin ich nicht einverstanden.
Betrachten wir die Menge A: alle geraden natürlichen Zahlen lassen sich Ausdrücken als (2n)
Betrachten wir nun die Menge B, diese muss sich auf jeden Fall aus der Menge der natürlichen Zahlen zusammensetzen.
Schauen wir uns zuerst die geraden natürlichen Zahlen an, also (2n) und bilden die Quadrate Eine gerade Zahl quadriert gibt wieder eine gerade Zahl
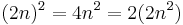
Vielfache von Zwei sind immer gerade.
-> Also sind alle geraden natürlichen Zahlen in Menge B enthalten.
Wenn wir uns nun die ungeraden natürlichen Zahlen betrachten, so sind die Quadrate der ungeraden natürlichen Zahlen immer wieder ungerade.
eine ungerade natürliche Zahl lässt sich darstellen als (2n-1)
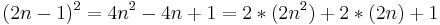
Aus dem letzten Audruck folgt, dass die Zahl ungerade sein muss, denn Vielfache von 2 sind immer gerade und zwei gerade Zahlen addiert sind auch gerade. Addiert man zu einer geraden Zahl 1 so ist sie ungerade.
-> Also sind die Mengen A und Mengen B gleich.
- Stimmt. --Jp1234 18:17, 19. Okt. 2010 (UTC)
- Wobei streng genommen auch die Teilmenge stimmt, denn jede Menge ist gleichzeitig Teilmenge von sich selbst und zwei Mengen sind genau dann gleich, wenn jede eine Teilmenge der anderen ist. Nur ist es keine echte Teilmenge.--Ridcully1975 21:52, 19. Okt. 2010 (UTC)

