Übungs Aufgaben 1 EG WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: ==Aufgabe 1.1== Im Skript wurde die Injektivität einer beliebigen Bewegung <math>\ \beta</math>mittels der Implikation (I)<math>\forall P_1, P_2 \in \epsilon \colon\...) |
|||
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
Diskutieren Sie den Zusammenhang zum indirekten Beweis der Implikation (I). | Diskutieren Sie den Zusammenhang zum indirekten Beweis der Implikation (I). | ||
| + | |||
| + | === Lösung von M.G.=== | ||
| + | demnächst | ||
| + | |||
| + | ==Aufgabe 1.2== | ||
| + | Beweisen Sie: Die Zwischenrelation ist eine Invariante bei Bewegungen. | ||
| + | |||
| + | [[Lösung von Aufgabe 1.2 WS2010]] | ||
| + | |||
| + | ==Aufgabe 1.3== | ||
| + | Beweisen Sie: Die Nacheinanderausführung zweier Bewegungen ist ein Bewegung. | ||
| + | |||
| + | [[Lösung von Aufgabe 1.3 WS2010)]] | ||
| + | [[Category:Elementargeometrie]] | ||
Aktuelle Version vom 16. November 2010, 22:58 Uhr
Inhaltsverzeichnis |
Aufgabe 1.1
Im Skript wurde die Injektivität einer beliebigen Bewegung 
mittels der Implikation
(I)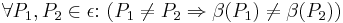
bewiesen.
Beweisen Sie die Injektitivät von noch einmal, indem Sie die Kontraposition von (I) beweisen.
Diskutieren Sie den Zusammenhang zum indirekten Beweis der Implikation (I).
Lösung von M.G.
demnächst
Aufgabe 1.2
Beweisen Sie: Die Zwischenrelation ist eine Invariante bei Bewegungen.
Aufgabe 1.3
Beweisen Sie: Die Nacheinanderausführung zweier Bewegungen ist ein Bewegung.
