Quiz der Woche 5 WS: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: Es sei <math>\ R</math> ein Äquivalenzrelation auf der Menge <math> \ M</math>. Wir zerlegen <math>\ M</math> derart in Teilmengen <math>\ T_1, T_2, T_3, ..., T_n, ......)
 
 
Zeile 28: Zeile 28:
 
(0) Weder <math>\ T_1</math> noch <math>\  T_2 </math> noch irgendeine andere der Mengen <math>\ T_1, T_2, T_3, ..., T_n, ...</math> ist { leer }.
 
(0) Weder <math>\ T_1</math> noch <math>\  T_2 </math> noch irgendeine andere der Mengen <math>\ T_1, T_2, T_3, ..., T_n, ...</math> ist { leer }.
 
</quiz>
 
</quiz>
 +
[[Category:Einführung_Geometrie]]

Aktuelle Version vom 16. November 2010, 23:09 Uhr

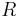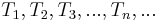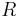Es sei \ R ein Äquivalenzrelation auf der Menge \ M. Wir zerlegen \ M derart in Teilmengen \ T_1, T_2, T_3, ..., T_n, ..., dass gilt: Jede der Teilmengen besteht aus all den Elementen von \ M, die in der Relation \ R zueinander stehen.
Satz:
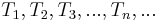Die Zerlegung von \ M in die Teilmengen \ T_1, T_2, T_3, ..., T_n, ... ist eine Klasseneinteilung von \ M.

Beispiel zu dieser Idee, Klassen einzuteilen

Pluspunkt für eine richtige Antwort:  
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1. Die Idee, eine Klasse durch eines ihrer Elemente zu beschreiben.
{Wir wollen versuchen, die Art und Weise der Generierung einer beliebigen der Teilmengen \ T_1, T_2, T_3, ..., T_n, ... formal zu beschreiben. Diesbezüglich stellen wir fest, dass es sinnvoller ist, nicht mit Zahlen, sondern Elementen aus \ M zu indizieren. Unter der Klasse \ T_a verstehen wir dann alle Elemente von \ M, die mit dem Element \ a aus M in der Relation \ R stehen. Welche der folgenden formalen Definitionen ist bezüglich dieser Idee korrekt?

\bigwedge_{a \in M}: T_a:= \lbrace b| b \in M \land bRa \rbrace
→ so liest sich das: Für alle a aus M legen wir die Teilmenge T_a derart fest, dass zu ihr alle Elemente b aus M gehören, die mit a in der Relation R stehen.
\bigwedge_{b \in M}: T_b:= \lbrace x| x \in M \land xRb \rbrace
→ Genau dasselbe wie zuvor, nur heißt a jetzt b und b dafür x.

2. Überlegungen zur Voraussetzung

Voraussetzung: R ist eine
Das bedeutet:
(R) R ist
(S) R ist
(T) R ist

3. Überlegungen zur Behauptung

Behauptung: Die Einteilung von \ M in die Teilmengen \ T_1, T_2, T_3, ..., T_n, ... ist eine von \ M.
Das bedeutet, dass wir zu zeigen haben:
(L) Der Durchschnitt zweier verschiedener Teilmengen \ T_i und \ T_j ist die
(S) Die Vereinigungsmenge aller Teilmengen \ T_1, T_2, T_3, ..., T_n, ... ist die Menge
(0) Weder \ T_1 noch \ T_2 noch irgendeine andere der Mengen \ T_1, T_2, T_3, ..., T_n, ... ist .

Punkte: 0 / 0
Von „http://geometrie.zum.de/index.php?title=Quiz_der_Woche_5_WS&oldid=5003“