Definitionen WS10/11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Definitionen) |
|||
| Zeile 24: | Zeile 24: | ||
=====Definition: (Parallelität von Geraden)===== | =====Definition: (Parallelität von Geraden)===== | ||
:Zwei Geraden sind paralle, wenn sie in derselben Ebene liegen und entweder keinen oder alle Punkte gemeinsam haben. | :Zwei Geraden sind paralle, wenn sie in derselben Ebene liegen und entweder keinen oder alle Punkte gemeinsam haben. | ||
| + | |||
| + | =====Definition I/4: (Inzidenz Gerade Ebene)===== | ||
| + | :Eine Gerade g gehört zu einer Ebene E, wenn jeder Punkt von g zu E gehört. | ||
| + | |||
| + | =====Definition I/5: (Raum)===== | ||
| + | :Die Menge aller Punkte P wird Raum genannt. | ||
| + | |||
| + | =====Definition I/6: (komplanar)===== | ||
| + | :Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(A, B, C, D, ...) (analog nkomp(..) für nicht komplanar) | ||
| + | |||
| + | =====Definition I/7: (komplanar für Geraden)===== | ||
| + | :Zwei Geraden g und h sind komplanar, wenn es eine Ebene gibt, in der beide Geraden vollständig liegen. | ||
| + | :Schreibweise: komp(g, h) | ||
| + | |||
| + | =====Definition I/8: (Geradenparallelität)===== | ||
| + | :Zwei Geraden g und h sind parallel, wenn sie identisch oder komplanar und schnittpunktfrei sind. | ||
| + | :In Zeichen: g||h. | ||
| + | |||
| + | =====Definition I/9: (windschief )===== | ||
| + | :Zwei Geraden g und h sind windschief, wenn sie schnittpunktfrei und nicht parallel sind. | ||
| + | |||
| + | =====Definition I/10: (parallel für Ebenen)===== | ||
| + | :Zwei Ebene E1 und E2 sind parallel, wenn sie keinen Punkt gemeinsam haben. | ||
Version vom 17. November 2010, 17:34 Uhr
Definitionen
Definition: (n-stellige Relation)
- Es seien
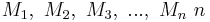Mengen, wobei keine dieser Mengen die leere Menge ist. Jede Teilmenge aus 
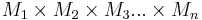ist eine 
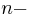stellige Relation.
Definition: (Klasseneinteilung eine Menge)
- Es sei
eine Menge und 
eine Menge 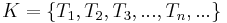von Teilmengen von .
ist eine Klasseneinteilung von , wenn
- notwendige Bedingung 1: Keine der Teilmengen ist die leere Menge.
- notwendige Bedingung 2: Je zwei Teilmengen sind disjunkt.
- notwendige Bedingung 3: Die Vereinigung aller Teilmengen ergibt wieder die Menge .
- Mengen sind disjukt, wenn die Schnittmenge dieser Mengen die leere Menge ist, bzw. die Mengen keine gemeinsamen Objekte besitzen.
Definition I/2: (kollinear)
- Eine Menge von Punkten heißt kollinear, wenn es eine Gerade gibt, die alle Punkte der Menge enthält.
- Schreibweise kolinear: koll(A, B, C, ...)
- Schreibweise nicht kollinear: nkoll(A, B, C)
Definition I/3: (Inzidenz Punkt Ebene)
- Ein Punkt P inzidiert mit einer Ebene E, wenn P ein Element der Ebene E ist.
Definition: (Parallelität von Geraden)
- Zwei Geraden sind paralle, wenn sie in derselben Ebene liegen und entweder keinen oder alle Punkte gemeinsam haben.
Definition I/4: (Inzidenz Gerade Ebene)
- Eine Gerade g gehört zu einer Ebene E, wenn jeder Punkt von g zu E gehört.
Definition I/5: (Raum)
- Die Menge aller Punkte P wird Raum genannt.
Definition I/6: (komplanar)
- Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(A, B, C, D, ...) (analog nkomp(..) für nicht komplanar)
Definition I/7: (komplanar für Geraden)
- Zwei Geraden g und h sind komplanar, wenn es eine Ebene gibt, in der beide Geraden vollständig liegen.
- Schreibweise: komp(g, h)
Definition I/8: (Geradenparallelität)
- Zwei Geraden g und h sind parallel, wenn sie identisch oder komplanar und schnittpunktfrei sind.
- In Zeichen: g||h.
Definition I/9: (windschief )
- Zwei Geraden g und h sind windschief, wenn sie schnittpunktfrei und nicht parallel sind.
Definition I/10: (parallel für Ebenen)
- Zwei Ebene E1 und E2 sind parallel, wenn sie keinen Punkt gemeinsam haben.
