Axiome WS10/11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Axiome) |
(→Axiome) |
||
| Zeile 2: | Zeile 2: | ||
*<u> '''Inzidenzaxiome:'''</u> | *<u> '''Inzidenzaxiome:'''</u> | ||
| + | |||
=====AXIOM I/0===== | =====AXIOM I/0===== | ||
| Zeile 30: | Zeile 31: | ||
=====Axiom I/7===== | =====Axiom I/7===== | ||
:Es gibt vier Punkte, die nicht komplanar sind. | :Es gibt vier Punkte, die nicht komplanar sind. | ||
| + | |||
| + | |||
| + | *<u> '''Abstandsaxiome:'''</u> | ||
| + | |||
| + | |||
| + | ===== Axiom II.1: (Abstandsaxiom) ===== | ||
| + | :Zu je zwei Punkten <math>\ A</math> und <math>\ B</math> gibt es eine eindeutig bestimmte nicht negative reelle Zahl <math>\ d</math> mit <math>d=0:\Longleftrightarrow A=B</math>. | ||
| + | |||
| + | ===== Axiom II.2: ===== | ||
| + | :Für zwei beliebige Punkte <math>\ A</math> und <math>\ B</math> gilt <math>\left| AB \right| = \left| BA \right|</math>. | ||
Version vom 21. November 2010, 12:39 Uhr
Inhaltsverzeichnis |
Axiome
- Inzidenzaxiome:
AXIOM I/0
- Geraden sind Punktmengen.
AXIOM I/1 (Axiom von der Geraden)
- Zu zwei beliebigen verschiedenen Punkten gibt es genau eine Gerade, die die beiden Punkte enthält.
- weitere Bezeichnungsmöglichkeit von Geraden
- Eine Gerade g, die durch zwei verschiedene Punkte A und B eindeutig bestimmt ist wird auch mit AB bezeichnet.
AXIOM I/2
- Zu jeder Geraden gibt es wenigstens zwei Punkte, die dieser Geraden angehören.
AXIOM I/3
- Es gibt wenigstens 3 Punkte, die nicht kollinear sind.
Axiom I/4
- Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, die diese drei Punkte enthält. Jede Ebene enthält (wenigstens) einen Punkt.
Axiom I/5
- Wenn zwei Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E.
Axiom I/6
- Wenn zwei Ebenen einen Punkt gemeinsam haben, so haben sie noch mindestens einen weiteren Punkt gemeinsam.
Axiom I/7
- Es gibt vier Punkte, die nicht komplanar sind.
- Abstandsaxiome:
Axiom II.1: (Abstandsaxiom)
- Zu je zwei Punkten
und 
gibt es eine eindeutig bestimmte nicht negative reelle Zahl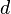 
mit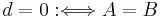 
.
Axiom II.2:
- Für zwei beliebige Punkte und gilt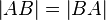
.
