Sätze WS10/11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(→Sätze) |
|||
| Zeile 23: | Zeile 23: | ||
=====Satz I.7:===== | =====Satz I.7:===== | ||
:Jede Ebene enthält (wenigstens) drei Punkte. | :Jede Ebene enthält (wenigstens) drei Punkte. | ||
| + | |||
| + | |||
| + | ===== Satz II.1 ===== | ||
| + | :Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{Zw} \left( C, B, A \right) </math>. | ||
| + | |||
| + | ===== Satz II.2: ===== | ||
| + | :Aus <math> \operatorname{Zw} \left( A, B, C \right) </math> folgt <math> \operatorname{koll} \left( A, B, C \right) </math>. | ||
| + | |||
| + | ===== Satz II.3 ===== | ||
| + | :Es sei <math> \operatorname{koll} \left( A, B, C \right) </math> mit <math>\ A, B, C</math> sind paarweise verschieden.<br /> Dann gilt <math> \operatorname{Zw} \left( A, B, C \right) </math> oder <math> \operatorname{Zw} \left( A, C, B \right) </math> oder <math> \operatorname{Zw} \left( B, A, C \right) </math>. | ||
| + | |||
| + | ===== Satz II.4 ===== | ||
| + | :Es sei <math>\ O</math> ein Punkt einer Geraden <math>\ g</math>. <br />Die Teilmengen <math> \ OA^+ \setminus \left\{ O \right\}</math>, <math> \left\{ O \right\}</math> und <math> \ OA^- \setminus \left\{ O \right\}</math> bilden eine Klasseneinteilung der Geraden <math>\ g</math>. | ||
Version vom 21. November 2010, 12:53 Uhr
Inhaltsverzeichnis |
Sätze
Hier geht es zu den Axiome WS10/11
Hier geht es zu den Definitionen WS10/11
Satz I.1
- Es seien g und h zwei Geraden. Wenn g und h nicht identisch sind, haben sie höchstens einen Punkt gemeinsam.
Satz I.2: (Kontraposition von Satz I.1)
- Es seien g und h zwei Geraden.
- Wenn g und h mehr als einen Punkt gemeinsam haben, so sind g und h identisch.
Satz I.3: (Existenz von drei Geraden)
- Es existieren mindestens drei paarweise verschiedene Geraden.
Satz I.5:
- Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Satz I.6:
- Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
Satz I.7:
- Jede Ebene enthält (wenigstens) drei Punkte.
Satz II.1
- Aus
folgt 
.
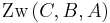Satz II.2:
- Aus folgt
.
Satz II.3
- Es sei mit
sind paarweise verschieden.
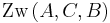Dann gilt oder 
oder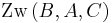 
.
Satz II.4
- Es sei
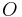ein Punkt einer Geraden 
.
Die Teilmengen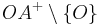
, 
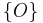und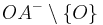 
bilden eine Klasseneinteilung der Geraden .
