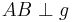Übungsaufgaben 3 EG WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2) |
||
| Zeile 3: | Zeile 3: | ||
Beweisen Sie: Wenn die beiden Geraden <math>\ g</math> und <math>\ h</math> den Punkt <math>\ Z</math> und nur den Punkt <math>\ Z</math> gemeinsam haben, dann gilt <math>S_h \circ S_g = D_{Z,\angle (g,h)}</math>. | Beweisen Sie: Wenn die beiden Geraden <math>\ g</math> und <math>\ h</math> den Punkt <math>\ Z</math> und nur den Punkt <math>\ Z</math> gemeinsam haben, dann gilt <math>S_h \circ S_g = D_{Z,\angle (g,h)}</math>. | ||
==Aufgabe 2== | ==Aufgabe 2== | ||
| − | Beweisen Sie: Wenn die beiden Geraden <math>\ g</math> und <math>\ h</math> parallel sind, dann ist die Nacheinanderausführung <math>S_h \circ S_g</math> die Verschiebung <math>V_\overrightarrow{AB}</math> mit <math>|\overrightarrow{AB}|=\frac{1}{2}|g,h|</math> | + | Beweisen Sie: Wenn die beiden Geraden <math>\ g</math> und <math>\ h</math> parallel sind, dann ist die Nacheinanderausführung <math>S_h \circ S_g</math> die Verschiebung <math>V_\overrightarrow{AB}</math> mit <math>|\overrightarrow{AB}|=\frac{1}{2}|g,h|</math> und <math>AB \perp g</math> |
Version vom 23. November 2010, 16:48 Uhr
Alle Aufgaben beziehen sich auf die ebene Geometrie.
Aufgabe 1
Beweisen Sie: Wenn die beiden Geraden  und
und  den Punkt
den Punkt  und nur den Punkt
und nur den Punkt  gemeinsam haben, dann gilt
gemeinsam haben, dann gilt 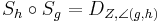 .
.
Aufgabe 2
Beweisen Sie: Wenn die beiden Geraden  und
und  parallel sind, dann ist die Nacheinanderausführung
parallel sind, dann ist die Nacheinanderausführung 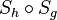 die Verschiebung
die Verschiebung 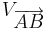 mit
mit 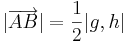 und
und