Übungsaufgaben 3 EG WS2010: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3) |
||
| Zeile 9: | Zeile 9: | ||
Es seien <math>\ Z_1</math> und <math>\ Z_2</math> zwei nicht identische Punkte. Ferner seien die Winkel <math>\ \alpha</math> und <math>\ \beta</math> supplementär. | Es seien <math>\ Z_1</math> und <math>\ Z_2</math> zwei nicht identische Punkte. Ferner seien die Winkel <math>\ \alpha</math> und <math>\ \beta</math> supplementär. | ||
| − | Man beweise: <math>D_{Z_2,\beta} \circ D_{Z_1, \alpha} = V_{2 \overrightarrow{Z_1Z_2}}</math> | + | Man beweise: <math>D_{Z_2,\beta} \circ D_{Z_1, \alpha} = V_{2 \overrightarrow{Z_1Z_2}}</math>. |
Version vom 23. November 2010, 16:08 Uhr
Alle Aufgaben beziehen sich auf die ebene Geometrie.
Aufgabe 1
Beweisen Sie: Wenn die beiden Geraden  und
und  den Punkt
den Punkt  und nur den Punkt
und nur den Punkt  gemeinsam haben, dann gilt
gemeinsam haben, dann gilt 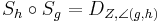 .
.
Aufgabe 2
Es seien  und
und  zwei zueinander parallele Geraden. Ferner sei
zwei zueinander parallele Geraden. Ferner sei  eine Gerade, die senkrecht auf
eine Gerade, die senkrecht auf  und damit auch senkrecht auf
und damit auch senkrecht auf  steht. Der Punkt
steht. Der Punkt  sei der Schnittpunkt von
sei der Schnittpunkt von  mit
mit  und der gemeinsame Schnittpunkt von
und der gemeinsame Schnittpunkt von  und
und  sei mit
sei mit 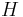 bezeichnet.
bezeichnet.
Man beweise: 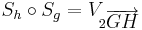 .
.
Aufgabe 3
Es seien 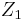 und
und 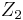 zwei nicht identische Punkte. Ferner seien die Winkel
zwei nicht identische Punkte. Ferner seien die Winkel  und
und  supplementär.
supplementär.
Man beweise: 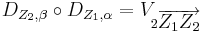 .
.

