Lösung von Aufg. 7.8: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 2: | Zeile 2: | ||
| + | Gegeben sei ein Kreis k. | ||
| + | Eine Strecke <math>\overline {AB}</math> ist dann eine Sehne des Kreises k, wenn <math>A \in k</math> und <math>B \in k</math><br /> | ||
| + | |||
| + | Eine Strecke <math>\overline {AB}</math> ist dann ein Durchmesser des Kreises k, wenn <math>A \in k</math>, <math>B \in k</math> und durch den Mittelpunkt M geht.<br /> | ||
| + | |||
| + | Eine Strecke <math>\overline {MA}</math> ist dann ein Radius des Kreises k, wenn <math>A \in k</math> | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 23. November 2010, 18:25 Uhr
Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser eines Kreises versteht.
Gegeben sei ein Kreis k.
Eine Strecke  ist dann eine Sehne des Kreises k, wenn
ist dann eine Sehne des Kreises k, wenn 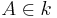 und
und 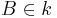
Eine Strecke  ist dann ein Durchmesser des Kreises k, wenn
ist dann ein Durchmesser des Kreises k, wenn 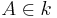 ,
, 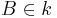 und durch den Mittelpunkt M geht.
und durch den Mittelpunkt M geht.
Eine Strecke 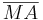 ist dann ein Radius des Kreises k, wenn
ist dann ein Radius des Kreises k, wenn