Lösung von Aufg. 7.3: Unterschied zwischen den Versionen

Version vom 23. November 2010, 19:25 Uhr

Satz:

Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.

1. Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
2. Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
3. Beweisen Sie den Satz. Hier ein Anfang für den Beweis:

Beweis

Es seien und 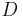drei Punkte, die nicht komplanar sind.

zu zeigen

...

Annahme:

Es gibt drei der Punkte vier Punkte , die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...

1) Wenn vier Punkte nicht in einer Ebene liegen, dann liegen je drei von ihnen nicht auf einer Geraden.

2) Vier Punkte sind nicht komplanar, falls je drei von ihnen nicht kollinear sind.

Vor: nkomp(A,B,C,D)
Beh: nkoll(A,B,C)

Annahme: koll(A,B,C)

Es gibt eine Gerade g mit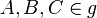

1.Fall: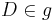

1) koll(A,B,C,D)________________________________laut Annahme

2) es existiert ein Punkt E mit_________________Axiom I/3
der Eigenschaft, dass E nicht Element von g ist

3) Zu je drei nichtkollinearen Punkten___________Axiom I/4 und 2)
o.B.d.A A,B,C gibt es genau eine Ebene E

4) mit 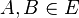gilt________________Axiom I/5 und 3)
) auch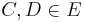

5) komp(A,B,C,D)__________________________________4)

6) Widerspruch zur Voraussetzung nkomp(A,B,C,D)

7) Annahme ist zu verwerfen
8) Behauptung stimmt

2. Fall D ist nicht Element g

1) koll(A,B,C)___________________________laut Annahme
2) D ist nicht Element g_________________laut Annahme
3) es existiert genau eine Ebene___________I/4 und 1) und 2)
E mit 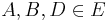4) 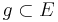_________________I/5 und 3)
5) komp(A, B,C,D)_________________________4)
6) Widerspruch zur Voraussetzung nkomp(A,B,C,D)
7) Annahme ist zu verwerfen
8) Behauptung stimmt