Lösung von Aufgabe 4.5: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
--> Na klar hat a einen Schnittpunkt mit sich selbst. Es sind unendlich viele Schnittpunkte. Also ist diese Relation reflexiv. | --> Na klar hat a einen Schnittpunkt mit sich selbst. Es sind unendlich viele Schnittpunkte. Also ist diese Relation reflexiv. | ||
| + | Wir betrachten hier ja die Schnittmenge zweier Geraden (Punktmengen) und die Schnittmenge zweier identischer Mengen<br />ist die Menge selbst und damit definitiv nicht leer, die Reflexivität gilt somit!--[[Benutzer:Schnirch|Schnirch]] 14:08, 24. Nov. 2010 (UTC) | ||
<u>Symmetrie:</u> aRb bRa<br /> | <u>Symmetrie:</u> aRb bRa<br /> | ||
stimmt<br /> | stimmt<br /> | ||
| − | --> Stimmt! Wenn a zu b einen Schnittpunkt hat, dann hat auch b zu a einen Schnittpunkt! | + | --> Stimmt! Wenn a zu b einen Schnittpunkt hat, dann hat auch b zu a einen Schnittpunkt!<br /> |
| + | korrekt!--[[Benutzer:Schnirch|Schnirch]] 14:08, 24. Nov. 2010 (UTC) | ||
<u>Transitivität:</u> aRb bRc draus folgt aRc<br /> | <u>Transitivität:</u> aRb bRc draus folgt aRc<br /> | ||
stimmt nicht--[[Benutzer:Engel82|Engel82]] 12:47, 4. Nov. 2010 (UTC) | stimmt nicht--[[Benutzer:Engel82|Engel82]] 12:47, 4. Nov. 2010 (UTC) | ||
--> Würde auch sagen stimmt nicht! a und c können parallel zueinander sein und beide von b geschnitten werden! | --> Würde auch sagen stimmt nicht! a und c können parallel zueinander sein und beide von b geschnitten werden! | ||
| + | auch das ist korrekt, die Transitivität gilt hier nicht--[[Benutzer:Schnirch|Schnirch]] 14:08, 24. Nov. 2010 (UTC) | ||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 24. November 2010, 15:08 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
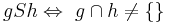
Reflexivität: aRa
stimmt
--> Ich würde sagen stimmt nicht, weil bei der Relation Schnittpunkt die Gerade a zu sich selbst doch keinen Schnittpunkt haben kann?!
--> Na klar hat a einen Schnittpunkt mit sich selbst. Es sind unendlich viele Schnittpunkte. Also ist diese Relation reflexiv.
Wir betrachten hier ja die Schnittmenge zweier Geraden (Punktmengen) und die Schnittmenge zweier identischer Mengen
ist die Menge selbst und damit definitiv nicht leer, die Reflexivität gilt somit!--Schnirch 14:08, 24. Nov. 2010 (UTC)
Symmetrie: aRb bRa
stimmt
--> Stimmt! Wenn a zu b einen Schnittpunkt hat, dann hat auch b zu a einen Schnittpunkt!
korrekt!--Schnirch 14:08, 24. Nov. 2010 (UTC)
Transitivität: aRb bRc draus folgt aRc
stimmt nicht--Engel82 12:47, 4. Nov. 2010 (UTC)
--> Würde auch sagen stimmt nicht! a und c können parallel zueinander sein und beide von b geschnitten werden!
auch das ist korrekt, die Transitivität gilt hier nicht--Schnirch 14:08, 24. Nov. 2010 (UTC)

