Lösung von Aufg. 8.1: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 11: Zeile 11:
 
existiert genau ein Punkt B* für den gilt:
 
existiert genau ein Punkt B* für den gilt:
 
<math>\left| AB^{*} \right| = \pi \left| AB \right|</math>
 
<math>\left| AB^{*} \right| = \pi \left| AB \right|</math>
−
5) Zw(A,B, B*), da <math>\pi </math>
+
5) Zw(A,B, B*), da <math>\pi </math> größer als 1 ist gilt:_____________4)
 +
<math>\overline{AB^{*}}</math> größer als <math>\overline{AB}</math><br />
 +
6)<math>\left| AB \right|</math>+\left|AB^{*}\right|=<math>\overline{AB^{*}}</math>

Version vom 30. November 2010, 20:06 Uhr

Beweisen Sie: Zu jeder Strecke \overline{AB} existiert genau eine Strecke \overline{AB^{*}} mit \left| AB^{*} \right| = \pi \left| AB \right| und \overline{AB} \subset \overline{AB^{*}}.


Vor: \overline{AB}
Beh: es existiert \overline{AB^{*}} mit \left| AB^{*} \right| = \pi \left| AB \right|;\overline{AB} \subset \overline{AB^{*}}.

1)\overline{AB}
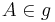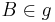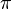__________________________________laut Vor 2) es existiert g: A \in g und B \in g_____Axiom I/1 3) es existier ein Strahl AB+______________________Def. Strahl 4) Auf dem Strahl AB+ mit dem Anfangspunkt A______________________Axiom vom Lineal existiert genau ein Punkt B* für den gilt: \left| AB^{*} \right| = \pi \left| AB \right| 5) Zw(A,B, B*), da \pi größer als 1 ist gilt:_____________4) \overline{AB^{*}} größer als \overline{AB}
6)\left| AB \right|+\left|AB^{*}\right|=\overline{AB^{*}}

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._8.1&oldid=5462“