Lösung von Aufg. 7.8: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
| − | Gegeben sei ein Kreis k. | + | Gegeben sei ein Kreis k und ein Mittelpunkt M. |
Eine Strecke <math>\overline {AB}</math> ist dann eine Sehne des Kreises k, wenn <math>A \in k</math> und <math>B \in k</math><br /> | Eine Strecke <math>\overline {AB}</math> ist dann eine Sehne des Kreises k, wenn <math>A \in k</math> und <math>B \in k</math><br /> | ||
| + | korrekt--[[Benutzer:Schnirch|Schnirch]] 14:02, 9. Dez. 2010 (UTC) | ||
Eine Strecke <math>\overline {AB}</math> ist dann ein Durchmesser des Kreises k, wenn <math>A \in k</math>, <math>B \in k</math> und durch den Mittelpunkt M geht.<br /> | Eine Strecke <math>\overline {AB}</math> ist dann ein Durchmesser des Kreises k, wenn <math>A \in k</math>, <math>B \in k</math> und durch den Mittelpunkt M geht.<br /> | ||
| + | im letzten Teil fehlt noch was: ... und '''die Strecke <math>\overline {AB}</math>''' durch den Mittelpunkt ''M'' verläuft.--[[Benutzer:Schnirch|Schnirch]] 14:02, 9. Dez. 2010 (UTC) | ||
| + | |||
| + | *Eine Strecke <math>\overline {AB}</math> ist dann ein Kreisdurchmesser, wenn eine Sehne <math>\overline {AB}</math> durch den Mittelpunkt M des Kreises k geht.* --[[Benutzer:Halikarnaz|Halikarnaz]] 11:13, 11. Dez. 2010 (UTC) | ||
Eine Strecke <math>\overline {MA}</math> ist dann ein Radius des Kreises k, wenn <math>A \in k</math>--[[Benutzer:Engel82|Engel82]] 17:26, 23. Nov. 2010 (UTC) | Eine Strecke <math>\overline {MA}</math> ist dann ein Radius des Kreises k, wenn <math>A \in k</math>--[[Benutzer:Engel82|Engel82]] 17:26, 23. Nov. 2010 (UTC) | ||
| + | das ist korrekt!--[[Benutzer:Schnirch|Schnirch]] 14:02, 9. Dez. 2010 (UTC) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
| + | |||
| + | Sehne: Wenn A und B zu dem Kreis k gehören, wird die Strecke <math>\overline {AB}</math> Kreissehne genannt.<br /> | ||
| + | ... Kreissehne '''des Kreises k''' genannt.--[[Benutzer:Schnirch|Schnirch]] 14:02, 9. Dez. 2010 (UTC) | ||
| + | |||
| + | Durchmesser: | ||
| + | <math>\overline {AM}</math> + <math>\overline {MB}</math> = <math>\overline {AB}</math>, wenn A und B Element k sind und M der Mittelpunkt des Kreises k ist.<br /> | ||
| + | korrekt!--[[Benutzer:Schnirch|Schnirch]] 14:02, 9. Dez. 2010 (UTC) | ||
| + | |||
| + | Radius:Eine Strecke <math>\overline {BM}</math> heißt dann Kreisradius, wenn der Punkt B auf dem Kreis k liegt und M der Mittelpunkt ist. | ||
| + | --[[Benutzer:Snoopy 1|Snoopy 1]] 14:29, 1. Dez. 2010 (UTC) | ||
| + | korrekt!--[[Benutzer:Schnirch|Schnirch]] 14:02, 9. Dez. 2010 (UTC) | ||
Aktuelle Version vom 11. Dezember 2010, 12:18 Uhr
Kreissehnen, Kreisradien und Kreisdurchmesser sind Strecken. Definieren Sie was man unter einer Sehne, einem Radius und einem Durchmesser eines Kreises versteht.
Gegeben sei ein Kreis k und ein Mittelpunkt M.
Eine Strecke 
ist dann eine Sehne des Kreises k, wenn 
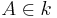und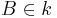 
korrekt--Schnirch 14:02, 9. Dez. 2010 (UTC)
Eine Strecke ist dann ein Durchmesser des Kreises k, wenn 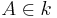, 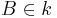und durch den Mittelpunkt M geht.
im letzten Teil fehlt noch was: ... und die Strecke
- Eine Strecke ist dann ein Kreisdurchmesser, wenn eine Sehne durch den Mittelpunkt M des Kreises k geht.* --Halikarnaz 11:13, 11. Dez. 2010 (UTC)
Eine Strecke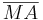 
ist dann ein Radius des Kreises k, wenn 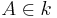--Engel82 17:26, 23. Nov. 2010 (UTC)
das ist korrekt!--Schnirch 14:02, 9. Dez. 2010 (UTC)
Sehne: Wenn A und B zu dem Kreis k gehören, wird die Strecke Kreissehne genannt.
... Kreissehne des Kreises k genannt.--Schnirch 14:02, 9. Dez. 2010 (UTC)
Durchmesser:
+ 
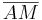= , wenn A und B Element k sind und M der Mittelpunkt des Kreises k ist.
korrekt!--Schnirch 14:02, 9. Dez. 2010 (UTC)
Radius:Eine Strecke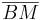 
heißt dann Kreisradius, wenn der Punkt B auf dem Kreis k liegt und M der Mittelpunkt ist.
--Snoopy 1 14:29, 1. Dez. 2010 (UTC)
korrekt!--Schnirch 14:02, 9. Dez. 2010 (UTC)
