Lösung von Aufg. 8.1: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \pi \left| AB \right|</math> und <math>\overline{AB} \subset \overline{AB^{*}}</math>.<br /> | Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \pi \left| AB \right|</math> und <math>\overline{AB} \subset \overline{AB^{*}}</math>.<br /> | ||
| + | == Lösung --[[Benutzer:Schnirch|Schnirch]] 14:00, 14. Dez. 2010 (UTC) == | ||
| + | Voraussetzung: Strecke <math>\overline{AB}\subset AB^+ </math> <br /> | ||
| + | Behauptung: es existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \pi \left| AB \right|</math> und <math>\overline{AB} \subset \overline{AB^{*}}</math> <br /> | ||
| + | {| class="wikitable " | ||
| + | |+ Beweis | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(I) | ||
| + | | es ex. genau ein Punkt <math> B^* \in AB^+ </math> mit <math>\left| AB^{*} \right| = \pi \left| AB \right|</math> | ||
| + | | Axiom III.1 | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(II) | ||
| + | | <math>\overline{AB^{*}}</math> existiert und ist eindeutig | ||
| + | | (I), Def. Strecke | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(III) | ||
| + | | <math>\left| AB^{*} \right| > \left| AB \right|</math> | ||
| + | | Rechnen in <math> \mathbb{R} </math> und <math> \pi </math> > 1 | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IV) | ||
| + | | <math> \operatorname{Zw} \left( A, B, B^* \right) </math> | ||
| + | | (I), (III), Def. Zw | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(V) | ||
| + | | <math>\overline{AB} \subset \overline{AB^{*}}</math> | ||
| + | | (IV) | ||
| + | |} | ||
| + | ==vorangegangene Lösungsversuche und Diskussionen== | ||
| + | <u>Vor:</u> <math>\overline{AB}</math> <br /> | ||
| + | <u>Beh:</u> es existiert <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \pi \left| AB \right|</math>;<math>\overline{AB} \subset \overline{AB^{*}}</math>.<br /> | ||
| − | |||
| − | |||
| − | 1)<math>\overline{AB}</math><br /> | + | 1)<math>\overline{AB}</math>__________________________________laut Vor<br /> |
| − | 2) es existiert g: <math>A \in g</math> und <math>B \in g</math>_____Axiom I/1 | + | 2) es existiert g: <math>A \in g</math> und <math>B \in g</math>_____Axiom I/1<br /> |
| − | 3) es | + | 3) es existiert ein Strahl AB+______________________Def. Strahl<br /> |
| − | 4) Auf dem Strahl AB+ mit dem Anfangspunkt A______________________Axiom vom Lineal | + | 4) Auf dem Strahl AB+ mit dem Anfangspunkt A______________________Axiom vom Lineal<br /> |
| − | existiert genau ein Punkt B* für den gilt: | + | existiert genau ein Punkt B* für den gilt:<br /> |
| − | <math>\left| AB^{*} \right| = \pi \left| AB \right|</math> | + | <math>\left| AB^{*} \right| = \pi \left| AB \right|</math><br /> |
| − | 5) Zw(A,B, B*), da <math>\pi </math> größer als 1 ist gilt:_____________4) | + | 5) Zw(A,B, B*), da <math>\pi </math> größer als 1 ist gilt:_____________4)<br /> |
<math>\overline{AB^{*}}</math> größer als <math>\overline{AB}</math><br /> | <math>\overline{AB^{*}}</math> größer als <math>\overline{AB}</math><br /> | ||
| − | 6)<math>\left| AB \right|</math>+\left| | + | 6)<math>\left| AB \right|</math>+ <math>\left|BB^{*}\right|</math> =<math>\left|AB^{*}\right|</math>___________Def. Zw und 5<br /> |
| + | 7)<math>\overline{AB}</math> für die gilt: (P/ Zw(A,P,B)<math>\cup</math>(A,B)________________Def. Strecke und 6)<br /> | ||
| + | 8)<math>\overline{AB^{*}}</math> für die gilt:(<math>\overline{AB}</math><math>\cup</math> (P/ Zw(B,P,B*))______Def. Strecke<br /> | ||
| + | 9)<math>\overline{AB} \subset \overline{AB^{*}}</math>.<br /> | ||
| + | 10)Behauptung stimmt--[[Benutzer:Engel82|Engel82]] 19:14, 30. Nov. 2010 (UTC) | ||
| + | <br /> | ||
| + | <br /> | ||
| + | Rückfragen zu diesem Beweis:<br /> | ||
| + | Woher weiß man, dass die drei Punkte auf ein und derselben Halbgerade liegen? Ist das nicht schon die Behauptung?<br /> | ||
| + | das ergibt sich aus 3) und 4)--[[Benutzer:Schnirch|Schnirch]] 14:00, 14. Dez. 2010 (UTC) | ||
| + | Wozu dient Schritt 6)?<br />--[[Benutzer:Jbo-sax|Jbo-sax]] 14:48, 7. Dez. 2010 (UTC)<br /> | ||
| + | richtig, dieser Schritt ist überflüssig - siehe Lösung oben--[[Benutzer:Schnirch|Schnirch]] 14:00, 14. Dez. 2010 (UTC) | ||
| + | |||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 14. Dezember 2010, 15:00 Uhr
Beweisen Sie: Zu jeder Strecke  existiert genau eine Strecke
existiert genau eine Strecke  mit
mit  und
und  .
.
Lösung --Schnirch 14:00, 14. Dez. 2010 (UTC)
Voraussetzung: Strecke 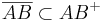
Behauptung: es existiert genau eine Strecke  mit
mit  und
und 
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | es ex. genau ein Punkt 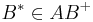 mit mit 
|
Axiom III.1 |
| (II) |  existiert und ist eindeutig existiert und ist eindeutig
|
(I), Def. Strecke |
| (III) | 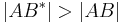
|
Rechnen in  und und 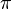 > 1 > 1
|
| (IV) | 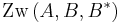
|
(I), (III), Def. Zw |
| (V) | 
|
(IV) |
vorangegangene Lösungsversuche und Diskussionen
Vor: 
Beh: es existiert  mit
mit  ;
; .
.
1) __________________________________laut Vor
__________________________________laut Vor
2) es existiert g: 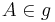 und
und 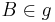 _____Axiom I/1
_____Axiom I/1
3) es existiert ein Strahl AB+______________________Def. Strahl
4) Auf dem Strahl AB+ mit dem Anfangspunkt A______________________Axiom vom Lineal
existiert genau ein Punkt B* für den gilt:

5) Zw(A,B, B*), da 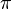 größer als 1 ist gilt:_____________4)
größer als 1 ist gilt:_____________4)
 größer als
größer als 
6) +
+ 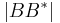 =
=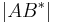 ___________Def. Zw und 5
___________Def. Zw und 5
7) für die gilt: (P/ Zw(A,P,B)
für die gilt: (P/ Zw(A,P,B)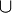 (A,B)________________Def. Strecke und 6)
(A,B)________________Def. Strecke und 6)
8) für die gilt:(
für die gilt:(
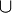 (P/ Zw(B,P,B*))______Def. Strecke
(P/ Zw(B,P,B*))______Def. Strecke
9) .
.
10)Behauptung stimmt--Engel82 19:14, 30. Nov. 2010 (UTC)
Rückfragen zu diesem Beweis:
Woher weiß man, dass die drei Punkte auf ein und derselben Halbgerade liegen? Ist das nicht schon die Behauptung?
das ergibt sich aus 3) und 4)--Schnirch 14:00, 14. Dez. 2010 (UTC)
Wozu dient Schritt 6)?
--Jbo-sax 14:48, 7. Dez. 2010 (UTC)
richtig, dieser Schritt ist überflüssig - siehe Lösung oben--Schnirch 14:00, 14. Dez. 2010 (UTC)

