Lösung von Aufg. 7.4: Unterschied zwischen den Versionen

Version vom 16. Dezember 2010, 15:47 Uhr

Beweisen Sie: Jede Ebene enthält wenigstens drei paarweise verschiedene Punkte.

Vor: Ebene $\epsilon$ ,nkomp(A,B,C,D)
Beh: $\epsilon$ enthält weinigstens drei paarweise verschiedene Punkte

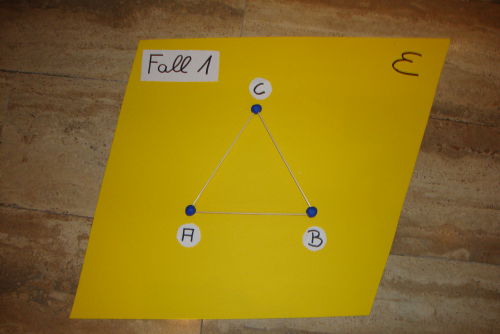
Fall 1:
3 der vier Punkte liegen in der Ebene $\epsilon$ $\rightarrow$ trivial

Fall 2:
2 der vier Punkte liegen in der Ebene $\epsilon$
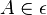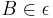
$A \in\epsilon$ , $B \in\epsilon$
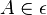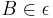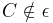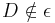
1) $A \in\epsilon$ , $B \in\epsilon$ , $C \notin\epsilon$ und $D \notin\epsilon$
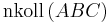
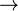
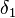2) $\operatorname{nkoll} \left( ABC \right)$ $\rightarrow$ $\delta_1$ ________Lemma 3 und Axiom I/4
3)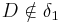 $D \notin\delta_1$ __________________wegen nkomp(A,B,C,D)
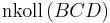
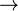
4) 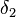$\operatorname{nkoll} \left( BCD \right)$ $\rightarrow$ $\delta_2$ ___________3)
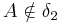5) $A \notin\delta_2$ ________________wegen nkomp(A,B,C,D)
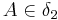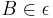6) $A \in\delta_2$ und $B \in\epsilon$ ____________2) und 4)
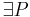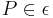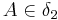7) $\exists P$ , $P \in\epsilon$ , $A \in\delta_2$ ________6) und Axiom I/6

bleibt zu zeigen : 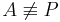$A\not\equiv P$
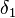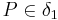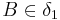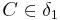
$\delta_1$ : $P \in\delta_1$ , $B \in\delta_1$ , $C \in\delta_1$
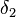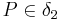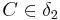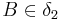
$\delta_2$ : $P \in\delta_2$ , $C \in\delta_2$ , $B \in\delta_2$
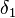
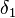
daraus folgt 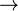$\delta_1$ $\equiv$ $\delta_1$ $\rightarrow$ komp(A,B,C,D)
8) Widerspruch zur Vorraussetzung nkomp(A,B,C,D)

3.Fall:
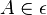1) $A \in\epsilon$ __________________Axiom I/4 und Lemma 3
2)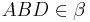 $ABD \in\beta$ __________________Axiom I/4 und Lemma 3
3)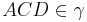 $ACD \in\gamma$ ________________da sonst A,B,C,D

Fall 4:
Keine der vier Punkte ist Element von $\epsilon$
$\epsilon$ enthält einen Punkt________nach Axiom I/4
$\rightarrow$ Fall 3

@@ Zeile 26: / Zeile 26: @@
 daraus folgt <math>\delta_1</math>  <math>\equiv </math> <math>\delta_1</math> <math>\rightarrow</math> komp(A,B,C,D)<br />
 ) Widerspruch zur Vorraussetzung nkomp(A,B,C,D)
 [[Bild:DSC02856.JPG|500px]]
 [[Bild:DSC02860.JPG|500px]]
+<u>3.Fall:</u><br />
+)<math>A \in\epsilon </math>__________________Axiom I/4 und Lemma 3<br />
+)<math>ABD \in\beta </math>__________________Axiom I/4 und Lemma 3<br />
+)<math>ACD \in\gamma </math>________________da sonst A,B,C,D
 [[Bild:DSC02849.JPG|500px]]

Lösung von Aufg. 7.4: Unterschied zwischen den Versionen

Version vom 16. Dezember 2010, 15:47 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge