Lösung von Aufg. 10.2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Jp1234 (Diskussion | Beiträge) |
|||
| Zeile 10: | Zeile 10: | ||
Eine Gerade g und eine Ebene <math>\epsilon</math> stehen senkrecht aufeinander, wenn es in <math>\epsilon</math> zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen.<br />--[[Benutzer:Engel82|Engel82]] 15:49, 15. Dez. 2010 (UTC) | Eine Gerade g und eine Ebene <math>\epsilon</math> stehen senkrecht aufeinander, wenn es in <math>\epsilon</math> zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen.<br />--[[Benutzer:Engel82|Engel82]] 15:49, 15. Dez. 2010 (UTC) | ||
| + | |||
| + | ... wenn es in <math>\epsilon</math> zwei voneinander verschiedene Geraden gibt, die senkrecht zu g stehen. --[[Benutzer:Jp1234|jp1234]] 23:35, 21. Dez. 2010 (UTC) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 22. Dezember 2010, 00:35 Uhr
Definition V.9 : (noch mehr Senkrecht)
- Eine Gerade
und eine Strecke 
stehen senkrecht aufeinander, wenn die und die Gerade 
senkrecht aufeinander stehen.
- Eine Gerade
Ergänzen Sie:
- Eine Strecke
und eine Strecke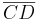 
stehen senkrecht aufeinander, wenn ... .
- Eine Strecke
- Eine Gerade und eine Ebene
stehen senkrecht aueinander, wenn es in ... .
- Eine Gerade
Eine Strecke und eine Strecke 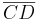stehen senkrecht aufeinander, wenn auch die Geraden und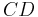 
senkrecht aufeinander stehen.
Eine Gerade g und eine Ebene stehen senkrecht aufeinander, wenn es in zwei Geraden gibt, die sich schneiden und jeweils senkrecht zu g stehen.
--Engel82 15:49, 15. Dez. 2010 (UTC)
... wenn es in zwei voneinander verschiedene Geraden gibt, die senkrecht zu g stehen. --jp1234 23:35, 21. Dez. 2010 (UTC)
