Lösung von Aufg. 10.5: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 10: Zeile 10:
 
5)<math>| \angle ASW| </math>= <math>\frac{1}{2} | \angle ASB |</math>_________________Rechnen in R und 4)<br />
 
5)<math>| \angle ASW| </math>= <math>\frac{1}{2} | \angle ASB |</math>_________________Rechnen in R und 4)<br />
 
6)<math>| \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |</math>.________________________1) und 5)--[[Benutzer:Engel82|Engel82]] 16:35, 15. Dez. 2010 (UTC)
 
6)<math>| \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |</math>.________________________1) und 5)--[[Benutzer:Engel82|Engel82]] 16:35, 15. Dez. 2010 (UTC)
 +
 +
----
 +
{| class="wikitable" 
 +
|1) Es existiert <math>\overline{SW} \subset\ {SW^+} </math>
 +
|Def. Strecke, Vor.<br />
 +
|-
 +
|2) <math>| \angle ASW| </math> = <math>| \angle WSB| </math>
 +
|Vor.
 +
|-
 +
|3) Es existiert <math> AB^+ \subset\ AB </math>
 +
|Axiom I/1, Def. Halbgerade
 +
|-
 +
|4) <math>| \angle AWS| </math> = 90
 +
|Winkelkonstruktionsaxiom
 +
|-
 +
|5) <math>| \angle AWS| </math> = <math>| \angle BWS| </math>
 +
|Supplementaxiom
 +
|-
 +
|6) <math>\overline{|AWS|} =  \overline{|BWS|} </math>
 +
|1), 2), 5), Kongruenzsatz WSW
 +
|-
 +
|7) <math>| \angle ASW| </math> + <math>| \angle WSB| </math> = <math>| \angle ASB|</math>
 +
|Winkeladditionsaxiom
 +
|-
 +
|8) 2<math>| \angle ASW| </math> = <math>| \angle ASB|</math>
 +
|2), Rechnen in R
 +
|-
 +
|9) <math>| \angle ASW| </math> = 1/2 <math>| \angle ASB|</math>
 +
|Rechnen in R
 +
|}
 +
 +
q.e.d.  --[[Benutzer:Pünktchen|Pünktchen]] 14:54, 16. Jan. 2011 (UTC)
  
  

Version vom 16. Januar 2011, 15:54 Uhr

Beweisen Sie Satz VI.eineinhalb 

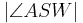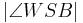Es sei \ SW^+ die Winkelhalbierende des Winkels \angle ASB. Dann gilt | \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |.


1)| \angle ASW| = | \angle WSB| __________________Def. Winkelhalbierende
2)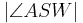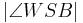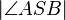| \angle ASW| +| \angle WSB| = | \angle ASB| ____________Winkeladditionsaxiom
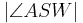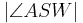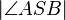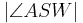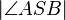3)| \angle ASW| +| \angle ASW| = | \angle ASB| ________________1) und 2)
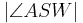4)2 | \angle ASW| = | \angle ASB| ____________________3)
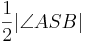5)| \angle ASW| = \frac{1}{2} | \angle ASB |_________________Rechnen in R und 4)
6)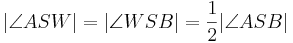| \angle ASW | = | \angle WSB | = \frac{1}{2} | \angle ASB |.________________________1) und 5)--Engel82 16:35, 15. Dez. 2010 (UTC)

1) Es existiert 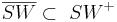\overline{SW} \subset\ {SW^+} Def. Strecke, Vor.
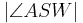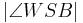
2) | \angle ASW| = | \angle WSB| Vor.
3) Es existiert 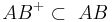AB^+ \subset\ AB Axiom I/1, Def. Halbgerade
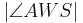4) | \angle AWS| = 90 Winkelkonstruktionsaxiom
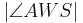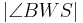
5) | \angle AWS| = | \angle BWS| Supplementaxiom
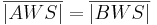
6) \overline{|AWS|} = \overline{|BWS|} 1), 2), 5), Kongruenzsatz WSW
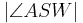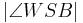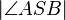
7) | \angle ASW| + | \angle WSB| = | \angle ASB| Winkeladditionsaxiom
8) 2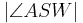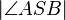| \angle ASW| = | \angle ASB| 2), Rechnen in R
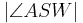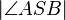
9) | \angle ASW| = 1/2 | \angle ASB| Rechnen in R

q.e.d. --Pünktchen 14:54, 16. Jan. 2011 (UTC)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._10.5&oldid=5963“