Aufgabe Kontinuum 01 WS 10 11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Mark behauptet: # Zu jedem Winkel α mit 0≤ α<2p gibt es genau einen Punkt B auf dem Kreis. # Zu jedem Punkt B gibt es genau eine Tangente an den Kreis. # Jede Ta...) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 2: | Zeile 2: | ||
| − | # Zu jedem Winkel α mit 0≤ α< | + | # Zu jedem Winkel α mit 0≤ α<2<math>\pi</math> gibt es genau einen Punkt B auf dem Kreis. |
# Zu jedem Punkt B gibt es genau eine Tangente an den Kreis. | # Zu jedem Punkt B gibt es genau eine Tangente an den Kreis. | ||
# Jede Tangente schneidet die x Achse in genau einem Punkt A. | # Jede Tangente schneidet die x Achse in genau einem Punkt A. | ||
| − | # Es gibt genau so viele Zahlen α mit 0≤ α< | + | # Es gibt genau so viele Zahlen α mit 0≤ α<2<math>\pi</math> wie Punkte auf der x-Achse. |
Version vom 24. Januar 2011, 22:53 Uhr
Mark behauptet:
- Zu jedem Winkel α mit 0≤ α<2
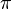 gibt es genau einen Punkt B auf dem Kreis.
gibt es genau einen Punkt B auf dem Kreis.
- Zu jedem Punkt B gibt es genau eine Tangente an den Kreis.
- Jede Tangente schneidet die x Achse in genau einem Punkt A.
- Es gibt genau so viele Zahlen α mit 0≤ α<2
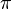 wie Punkte auf der x-Achse.
wie Punkte auf der x-Achse.

