Aufgabe Kontinuum 01 WS 10 11: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 8: Zeile 8:
  
 
<ggb_applet width="892" height="492"  version="3.2" ggbBase64="UEsDBBQACAAIAOC2OD4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VjbbuM2EH3ufgWhdzui7gLsXTjJywJpAzTbfehLQUm0zUYSXZJK7PzV/sh+U4cX2YovqZNdtNsAgaQhNRyec2aG8uTDuqnRAxWS8Xbq4bHvIdqWvGLtYup1aj7KvA/v300WlC9oIQiac9EQNfXCceBpe8fev/tpIpf8EZHaTPnM6OPUm5NaUg/JlaCkkktK1TM76dasZkRsbos/aankbsA6+diuOlhFiQ5sZVPdMNk/XpgFVzVT1+yBVVSgmpdTL4khdLj7TIViJamnXuRbSzD1gr1BMIV6dMkFe+Kt0tN3zudgQUiyJwpv+to2uTAbndCurFnFSKs3Y+KASQg9skotp16WB+CSssUSYo1y33orORfV3UYq2qD171RwWDvJx2GahfAf55mfZx7a2JEgS8dZGPlxEgZRlOEUIIR4IRCM87Gf+WmU+VmepDgK4aXTY2Zp+nBHlQIqJSJrKns8F4JVW8D1w0d5yeudacVZq67ISnXCyCB0pju10asBbkLvcdYuaupssPFyScv7gq/vDG44tK4/bVbmFRNPsbjiNRdIaEZimOCuhb2aOTrQ7SzfzPHNDOdDO92OY434wl0LezWzatba0NzGcb9r7PfLMIm0AZxr9fbY1KSgIAYPdS1TN/0DiObe7RTb+b90TQFZM5TN1iX+Ti4nF3t6m9xT0dLaqqoFYjveSfSg1WupM3FUtGQNPNoBBwjRZP0GAVhrRReC9nHblLNwmdFnyj0wS0UEkA9rKCgadmgXch+ijlCCuTSTFFN6pzrxFSSdvquI0hadVTVtKKScMloxUtuidutt6ws3pWIP1R38MHxUN0ZhpF4tCVjGbg812UDhGO7K+LudzyVVaD31RoFOStA+Hgz/zKvnUJAtCpDeK+1fc7mitHK1VDn5oxWsaJJpQJTBV+rVdFx6NXN9su+aKTbvdJExy4ZOFhYwA3LTkLZCLWlgnSsmypoaxJguoIj4GkFE8MAl71Q/VFp3zskBE8AgK7dIl97zxFJLUHBLpTTZr4Z5fpquwe5P8eWfzdYBHWcFB/WZtg8QGhcSobXvmNr4Pfy9ZQ2ojSwzDj/0NAQSmBdsjWb9/Fk/awbtZWTvQud0FvW+ZrG7s8H81dqApS0FoJ2SzVm5z/NzYkwybzH9+uUPbLgBKDoHCB6HCQ7jJMNJDH9p6oipTcNsWOviagioLxkHWYizOPRTnOZxlgADheR1p+hdCWWiveGlUXlPput3YWJ8gIcIOwFH9m7O1nTXT4532bflNPYPVYLPVAl+hUqIKAdpdzLdfZxGcRjkQYzzPIKb+Fj+40H+D4r7iSz+2CpoAwDLXiKXNpHXM+gzB6l8ZQevX87o57X16h9q64lkTSLDhL4U9vLWfN0VwBF+awV8aYPXP84G+/2NvrHE/8oV9M09ZVxb8k0hQCTQNX9fH5evEcblm5rum2HbdV3bc0c4OA9Ufxz4aY5xkvtwVE7jPIqdiPI0w1Ga+H4ahhmcpr8FcnPOPY74rYX78gDur19exnu/gp9bv/+lmjk4B8EBSEOaf9+KqkNyh8+aP/5K5zVdG5z3j5OnSLmjC20/ftY55KN4mQ7pvPVoFj/+WWdQO4/JfXMiO56GS511XNo7obAGPr1LprYQ17qvbXsWNMfDL5J7Slf6Q/C2/SRIK/VvCOfyfCvge2HBW1LfQLR7dF9auosDusnLdOuNb2ki/zOuj5e8oyIY1rxvJvv1BxZ7UjEUkQOKZq9pSLP/qiGNMHYtKX5jnz9G2FlN6GL4AW1+gnK/wb3/G1BLBwjkiStWOAUAALUTAABQSwECFAAUAAgACADgtjg+5IkrVjgFAAC1EwAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAHIFAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
 
<ggb_applet width="892" height="492"  version="3.2" ggbBase64="UEsDBBQACAAIAOC2OD4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VjbbuM2EH3ufgWhdzui7gLsXTjJywJpAzTbfehLQUm0zUYSXZJK7PzV/sh+U4cX2YovqZNdtNsAgaQhNRyec2aG8uTDuqnRAxWS8Xbq4bHvIdqWvGLtYup1aj7KvA/v300WlC9oIQiac9EQNfXCceBpe8fev/tpIpf8EZHaTPnM6OPUm5NaUg/JlaCkkktK1TM76dasZkRsbos/aankbsA6+diuOlhFiQ5sZVPdMNk/XpgFVzVT1+yBVVSgmpdTL4khdLj7TIViJamnXuRbSzD1gr1BMIV6dMkFe+Kt0tN3zudgQUiyJwpv+to2uTAbndCurFnFSKs3Y+KASQg9skotp16WB+CSssUSYo1y33orORfV3UYq2qD171RwWDvJx2GahfAf55mfZx7a2JEgS8dZGPlxEgZRlOEUIIR4IRCM87Gf+WmU+VmepDgK4aXTY2Zp+nBHlQIqJSJrKns8F4JVW8D1w0d5yeudacVZq67ISnXCyCB0pju10asBbkLvcdYuaupssPFyScv7gq/vDG44tK4/bVbmFRNPsbjiNRdIaEZimOCuhb2aOTrQ7SzfzPHNDOdDO92OY434wl0LezWzatba0NzGcb9r7PfLMIm0AZxr9fbY1KSgIAYPdS1TN/0DiObe7RTb+b90TQFZM5TN1iX+Ti4nF3t6m9xT0dLaqqoFYjveSfSg1WupM3FUtGQNPNoBBwjRZP0GAVhrRReC9nHblLNwmdFnyj0wS0UEkA9rKCgadmgXch+ijlCCuTSTFFN6pzrxFSSdvquI0hadVTVtKKScMloxUtuidutt6ws3pWIP1R38MHxUN0ZhpF4tCVjGbg812UDhGO7K+LudzyVVaD31RoFOStA+Hgz/zKvnUJAtCpDeK+1fc7mitHK1VDn5oxWsaJJpQJTBV+rVdFx6NXN9su+aKTbvdJExy4ZOFhYwA3LTkLZCLWlgnSsmypoaxJguoIj4GkFE8MAl71Q/VFp3zskBE8AgK7dIl97zxFJLUHBLpTTZr4Z5fpquwe5P8eWfzdYBHWcFB/WZtg8QGhcSobXvmNr4Pfy9ZQ2ojSwzDj/0NAQSmBdsjWb9/Fk/awbtZWTvQud0FvW+ZrG7s8H81dqApS0FoJ2SzVm5z/NzYkwybzH9+uUPbLgBKDoHCB6HCQ7jJMNJDH9p6oipTcNsWOviagioLxkHWYizOPRTnOZxlgADheR1p+hdCWWiveGlUXlPput3YWJ8gIcIOwFH9m7O1nTXT4532bflNPYPVYLPVAl+hUqIKAdpdzLdfZxGcRjkQYzzPIKb+Fj+40H+D4r7iSz+2CpoAwDLXiKXNpHXM+gzB6l8ZQevX87o57X16h9q64lkTSLDhL4U9vLWfN0VwBF+awV8aYPXP84G+/2NvrHE/8oV9M09ZVxb8k0hQCTQNX9fH5evEcblm5rum2HbdV3bc0c4OA9Ufxz4aY5xkvtwVE7jPIqdiPI0w1Ga+H4ahhmcpr8FcnPOPY74rYX78gDur19exnu/gp9bv/+lmjk4B8EBSEOaf9+KqkNyh8+aP/5K5zVdG5z3j5OnSLmjC20/ftY55KN4mQ7pvPVoFj/+WWdQO4/JfXMiO56GS511XNo7obAGPr1LprYQ17qvbXsWNMfDL5J7Slf6Q/C2/SRIK/VvCOfyfCvge2HBW1LfQLR7dF9auosDusnLdOuNb2ki/zOuj5e8oyIY1rxvJvv1BxZ7UjEUkQOKZq9pSLP/qiGNMHYtKX5jnz9G2FlN6GL4AW1+gnK/wb3/G1BLBwjkiStWOAUAALUTAABQSwECFAAUAAgACADgtjg+5IkrVjgFAAC1EwAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAHIFAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
 +
<br /><br /><br />
 +
Man kommentiere die "Beweisführung" von Mark.

Version vom 24. Januar 2011, 22:56 Uhr

Mark behauptet:


  1. Zu jedem Winkel α mit 0≤ α<2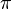\pi gibt es genau einen Punkt B auf dem Kreis.
  2. Zu jedem Punkt B gibt es genau eine Tangente an den Kreis.
  3. Jede Tangente schneidet die x Achse in genau einem Punkt A.
  4. Es gibt genau so viele reelle Zahlen α mit 0≤ α<2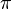\pi wie Punkte auf der x-Achse.




Man kommentiere die "Beweisführung" von Mark.

Von „http://geometrie.zum.de/index.php?title=Aufgabe_Kontinuum_01_WS_10_11&oldid=6126“