Lösung von Aufg. 13.5: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 1: | Zeile 1: | ||
Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt. Dieser Punkt ist der Mittelpunkt des Umkreises des Dreiecks. | Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt. Dieser Punkt ist der Mittelpunkt des Umkreises des Dreiecks. | ||
| − | Vor:<math>\triangle {AMP}</math> | + | Vor:<math>\triangle {AMP}</math><br /> |
| − | Beh: mab,mbc,mac schneiden sich in einem Punkt | + | Beh: mab,mbc,mac schneiden sich in einem Punkt<br /> |
| + | |||
| + | 1) Für alle Punkte X der mab der Seite <math>\overline {AB}</math> gilt:____________Mittelsenkrechtenkriterium<br /> | ||
| + | |<math>{AX}</math>|=|<math>{BX}</math>| <br /> | ||
| + | |||
| + | 2)Für alle Punkte X der mac der Seite <math>\overline {AC}</math> gilt:____________Mittelsenkrechtenkriterium<br /> | ||
| + | |<math>{AX}</math>|=|<math>{CX}</math>|<br /> | ||
| + | 3) Für den Schnittpunkt P der mab und mac gilt:____________________________2), 3)<br /> | ||
| + | |<math>{AP}</math>|= |<math>{BP}</math>|=|<math>{CP}</math>|<br /> | ||
| + | 4)|<math>{CP}</math>|=|<math>{BP}</math>|_____________________Mittelsenkrechtenkriterium | ||
| + | <math>P \in mbc</math><br /> | ||
| + | 5) P ist der Schnittpunkt der drei Mittelsenkrechten_________________3),4)<br /> | ||
| + | mab, mbc,mac. --[[Benutzer:Engel82|Engel82]] 18:00, 25. Jan. 2011 (UTC) | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| − | |||
| − | |||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 25. Januar 2011, 19:00 Uhr
Beweisen Sie: Die Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt. Dieser Punkt ist der Mittelpunkt des Umkreises des Dreiecks.
Vor: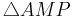
Beh: mab,mbc,mac schneiden sich in einem Punkt
1) Für alle Punkte X der mab der Seite  gilt:____________Mittelsenkrechtenkriterium
gilt:____________Mittelsenkrechtenkriterium
|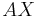 |=|
|=|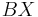 |
|
2)Für alle Punkte X der mac der Seite  gilt:____________Mittelsenkrechtenkriterium
gilt:____________Mittelsenkrechtenkriterium
|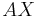 |=|
|=|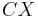 |
|
3) Für den Schnittpunkt P der mab und mac gilt:____________________________2), 3)
|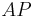 |= |
|= |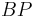 |=|
|=|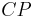 |
|
4)|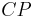 |=|
|=|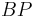 |_____________________Mittelsenkrechtenkriterium
|_____________________Mittelsenkrechtenkriterium
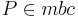
5) P ist der Schnittpunkt der drei Mittelsenkrechten_________________3),4)
mab, mbc,mac. --Engel82 18:00, 25. Jan. 2011 (UTC)

