Eigenschaften von Geraden So Se 11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Synthetische Geometrie) |
*m.g.* (Diskussion | Beiträge) (→Anzahl der geraden durch zwei verschiedene Punkte) |
||
| Zeile 4: | Zeile 4: | ||
<ggb_applet width="800" height="600" version="3.2" ggbBase64="UEsDBBQACAAIAFF7pz4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVZNb9swDD2vv0LQvY4/kiIF7Bb92KFAtx3S9bCbbDO2VtkKJDl1+utHSbaTFAOGATkkF1mPNPkeRcpJb/tGkC0ozWWb0SgIKYG2kCVvq4x2Zn25pLc3F2kFsoJcMbKWqmEmo0kQU4t3/ObiS6pr+U6YcC6vHN4zumZCAyV6o4CVugYwRzjrei44U7sf+W8ojN4bfJCndtNhFqM6xIqmfOZ63M5cwo3g5pFveQmKCFlk9GqB1PHpFZThBRMZnYceiTMafzIilFhrLRX/kK2x7vvga0QI0fwDsCKxxdKZE5pCVwhectZaMY4HOhHyzktTZ3R5HWNI4FWNXBdR6KMVUqpytdMGGtL/AiWRTrSwhd75XeJ3GnlhwkXoTIc7Fwa2KzAGj0UT1sO+YJXi5dHmSd9LsYc2krfmgW1Mp9yZJgO0MjubAHMpS/iurQQMGKooaijectmvfBESH/plt3GvOEJ59SCFVETZ8i7QYVhzvzofy3TyCp1P6DyGGDboZI9s+aphzf3qvARvPbVBeTSqHkvMeq6JBWwZsRUn8YLlgEdLSddy8zxusAXeBqmRf+F71+Q4A4dNMMWMThUznX1qn/QNVAvCN0mLZ9vJTpOtbUafyxEpoeANbr1hKAmzx/UTCXi0hErBSNxPkC+Ysx414ic4nY0kLAeNXAuDVwHqMVaLnVSDU2KfSmYsYsdAQAM4I8b1g2unqS53dLoQpJvtcYoH+77CaP5rb7guYmJTM0TG9hdsh5N+KMfF+ybLY5Fr3kPpkX0mp1yTPqOXYYDBd/b+CpeUfPgrzzn5qbDz7N5OhiPzUv8h+v6sRc+DJHai4yA6neaHs9YcBvO504wnfn11OtWPZ616HsST6vCEqr+eteooWC7Dw1/kajAPFv854rPDK9B99Ye/PTd/AFBLBwjsP5LLrQIAACgJAABQSwECFAAUAAgACABRe6c+7D+Sy60CAAAoCQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAOcCAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="800" height="600" version="3.2" ggbBase64="UEsDBBQACAAIAFF7pz4AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVZNb9swDD2vv0LQvY4/kiIF7Bb92KFAtx3S9bCbbDO2VtkKJDl1+utHSbaTFAOGATkkF1mPNPkeRcpJb/tGkC0ozWWb0SgIKYG2kCVvq4x2Zn25pLc3F2kFsoJcMbKWqmEmo0kQU4t3/ObiS6pr+U6YcC6vHN4zumZCAyV6o4CVugYwRzjrei44U7sf+W8ojN4bfJCndtNhFqM6xIqmfOZ63M5cwo3g5pFveQmKCFlk9GqB1PHpFZThBRMZnYceiTMafzIilFhrLRX/kK2x7vvga0QI0fwDsCKxxdKZE5pCVwhectZaMY4HOhHyzktTZ3R5HWNI4FWNXBdR6KMVUqpytdMGGtL/AiWRTrSwhd75XeJ3GnlhwkXoTIc7Fwa2KzAGj0UT1sO+YJXi5dHmSd9LsYc2krfmgW1Mp9yZJgO0MjubAHMpS/iurQQMGKooaijectmvfBESH/plt3GvOEJ59SCFVETZ8i7QYVhzvzofy3TyCp1P6DyGGDboZI9s+aphzf3qvARvPbVBeTSqHkvMeq6JBWwZsRUn8YLlgEdLSddy8zxusAXeBqmRf+F71+Q4A4dNMMWMThUznX1qn/QNVAvCN0mLZ9vJTpOtbUafyxEpoeANbr1hKAmzx/UTCXi0hErBSNxPkC+Ysx414ic4nY0kLAeNXAuDVwHqMVaLnVSDU2KfSmYsYsdAQAM4I8b1g2unqS53dLoQpJvtcYoH+77CaP5rb7guYmJTM0TG9hdsh5N+KMfF+ybLY5Fr3kPpkX0mp1yTPqOXYYDBd/b+CpeUfPgrzzn5qbDz7N5OhiPzUv8h+v6sRc+DJHai4yA6neaHs9YcBvO504wnfn11OtWPZ616HsST6vCEqr+eteooWC7Dw1/kajAPFv854rPDK9B99Ye/PTd/AFBLBwjsP5LLrQIAACgJAABQSwECFAAUAAgACABRe6c+7D+Sy60CAAAoCQAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAOcCAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
==Analytische Geometrie== | ==Analytische Geometrie== | ||
| − | ===Anzahl der | + | ===Anzahl der Geraden durch zwei verschiedene Punkte=== |
Definition: (Gerade im <math>\mathbb{R} ^2</math>) | Definition: (Gerade im <math>\mathbb{R} ^2</math>) | ||
| − | ::Es seien <math>a, b, c \in \mathbb{R} </math> mit <math>a^2+b^2\neq 0</math> | + | ::Es seien <math>a, b, c \in \mathbb{R} </math> mit <math>a^2+b^2\neq 0</math>. Unter einer Geraden versteht man die Menge aller Punkte <math>P(x_p,y_p)</math> mit <math>ax_p+by_p+c=0</math>. |
| + | |||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 7. Mai 2011, 14:45 Uhr
Inhaltsverzeichnis |
Synthetische Geometrie
Anzahl der Geraden durch zwei verschiedene Punkte
Aufgabe: Konstruiere alle Geraden die durch jeweils zwei der folgenden Punkte gehen:
Analytische Geometrie
Anzahl der Geraden durch zwei verschiedene Punkte
Definition: (Gerade im 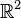 )
)
- Es seien
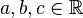 mit
mit 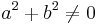 . Unter einer Geraden versteht man die Menge aller Punkte
. Unter einer Geraden versteht man die Menge aller Punkte 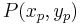 mit
mit 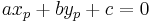 .
.
- Es seien

