Eigenschaften von Geraden So Se 11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Anzahl der Geraden durch zwei verschiedene Punkte) |
*m.g.* (Diskussion | Beiträge) (→Anzahl der Geraden durch zwei verschiedene Punkte) |
||
| Zeile 7: | Zeile 7: | ||
Definition: (Gerade im <math>\mathbb{R} ^2</math>) | Definition: (Gerade im <math>\mathbb{R} ^2</math>) | ||
::Es seien <math>a, b, c \in \mathbb{R} </math> mit <math>a^2+b^2\neq 0</math>. Unter einer Geraden versteht man die Menge aller Punkte <math>\ P(x_p,y_p)</math> mit <math>\ ax_p+by_p+c=0</math>. | ::Es seien <math>a, b, c \in \mathbb{R} </math> mit <math>a^2+b^2\neq 0</math>. Unter einer Geraden versteht man die Menge aller Punkte <math>\ P(x_p,y_p)</math> mit <math>\ ax_p+by_p+c=0</math>. | ||
| + | Aufgabe: Beweisen Sie: Durch zwei verschiedene Punkte <math>\ A(x_A, y_A), B(x_B,y_B)</math> gibt es genau eine Gerade. | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 7. Mai 2011, 14:48 Uhr
Inhaltsverzeichnis |
Synthetische Geometrie
Anzahl der Geraden durch zwei verschiedene Punkte
Aufgabe: Konstruiere alle Geraden die durch jeweils zwei der folgenden Punkte gehen:
Analytische Geometrie
Anzahl der Geraden durch zwei verschiedene Punkte
Definition: (Gerade im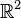 
)
- Es seien
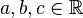mit 
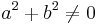. Unter einer Geraden versteht man die Menge aller Punkte 
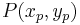mit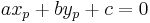 
.
- Es seien
Aufgabe: Beweisen Sie: Durch zwei verschiedene Punkte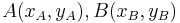 
gibt es genau eine Gerade.
