Lösung von Aufgabe 3.3 (SoSe11): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(3 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt)
Zeile 11: Zeile 11:
  
 
Wie geht man da vor? bzw. wie fange ich da an? Hat jemand ne ahnung? --[[Benutzer:Nitnelav12|Nitnelav12]] 16:16, 27. Apr. 2011 (CEST)
 
Wie geht man da vor? bzw. wie fange ich da an? Hat jemand ne ahnung? --[[Benutzer:Nitnelav12|Nitnelav12]] 16:16, 27. Apr. 2011 (CEST)
 +
 +
s. Diskussion --[[Benutzer:*m.g.*|*m.g.*]] 23:53, 27. Apr. 2011 (CEST)
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]
 +
[[Link-Text]]<br /><br />
 +
 +
'''Lösung:'''<br />
 +
 +
zu zeigen:  <MSP = <MSQ <br />
 +
 +
(1) Strecke SQ = Strecke SP              Konstruktionsvorschrift <br />
 +
(2) Strecke PM = Strecke MQ              Konstruktionsvorschrift, Def Mittelpunkt <br />
 +
(3) Strecke SM = Strecke SM              trivial <br />
 +
(4) Dreieck SMQ = Dreieck SMP            SSS, (1),(2),(3) <br />
 +
(5) <MSP = <MSQ                          (4) <br /> 
 +
q.e.d.[[Benutzer:Mathegott|Mathegott]] 18:18, 7. Jun. 2011 (CEST)
 +
 +
Die Lösung von Mathegott ist prinzipiell richtig, allerdings sollten Sie in Schritt 4 und 5 das Kongruenzzeichen (<math>\cong</math>) und nicht<br /> das Gleichheitszeichen benutzen.--[[Benutzer:Schnirch|Schnirch]] 14:01, 9. Jun. 2011 (CEST)
 +
[[Kategorie:Einführung_Geometrie]]

Aktuelle Version vom 9. Juni 2011, 13:02 Uhr

Wir gehen von folgender Definition aus:
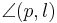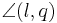Eine Winkelhalbierende eines Winkels \angle (p,q) ist ein Strahl l, der im Inneren des Winkels \angle (p,q) liegt, den Scheitel des Winkels \angle (p,q) als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel \angle (p,l) und \angle (l,q) unterteilt.
Außerdem sei folgende genetische Definition gegeben:

  • Gegeben sei ein Winkel \angle (p,q).
  • Man konstruiere auf den beiden Schenkeln des Winkels \angle (p,q) zwei Punkte P und Q, die vom Scheitel S des Winkels \angle (p,q) gleich weit entfernt sind.
  • Man konstruiere die Strecke \overline{PQ}.
  • Man konstruiere den Mittelpunkt M der Strecke \overline{PQ}.
  • Man konstruiere den Strahl w mit dem Anfangspunkt S, der durch den Punkt M verläuft.
  • Dieser Strahl w ist die Winkelhalbierende.

Beweisen Sie, dass durch diese Konstruktionsvorschrift tatsächlich die Winkelhalbierende entsprechend der angegebenen Definition entsteht.

Wie geht man da vor? bzw. wie fange ich da an? Hat jemand ne ahnung? --Nitnelav12 16:16, 27. Apr. 2011 (CEST)

s. Diskussion --*m.g.* 23:53, 27. Apr. 2011 (CEST)Link-Text

Lösung:

zu zeigen: <MSP = <MSQ

(1) Strecke SQ = Strecke SP Konstruktionsvorschrift
(2) Strecke PM = Strecke MQ Konstruktionsvorschrift, Def Mittelpunkt
(3) Strecke SM = Strecke SM trivial
(4) Dreieck SMQ = Dreieck SMP SSS, (1),(2),(3)
(5) <MSP = <MSQ (4)
q.e.d.Mathegott 18:18, 7. Jun. 2011 (CEST) 

Die Lösung von Mathegott ist prinzipiell richtig, allerdings sollten Sie in Schritt 4 und 5 das Kongruenzzeichen (\cong) und nicht
 das Gleichheitszeichen benutzen.--Schnirch 14:01, 9. Jun. 2011 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_3.3_(SoSe11)&oldid=7629“