|
|
| Zeile 15: |
Zeile 15: |
| | Den Rest können Sie alleine ... . | | Den Rest können Sie alleine ... . |
| | | | |
| − | ===Lösungsmöglichkeit 1===
| |
| − | {| class="wikitable"
| |
| − | |-
| |
| − | |<u>Voraussetzung:</u>|| Existenz von A, B, C mit A ungleich B, B ungleich C , C ungleich A und Zw (A, B, C)
| |
| − | |-
| |
| − | |<u>Behauptung:</u>|| <math>\ |A'B'| + |B'C'| = |A'C'|</math>
| |
| − | |}
| |
| | | | |
| − | | + | [[Kategorie:Elementargeometrie]] |
| − | {| class="wikitable center"
| + | |
| − | |- style="background: #DDFFDD;"
| + | |
| − | ! Nr.
| + | |
| − | ! Beweisschritt
| + | |
| − | ! Begründung
| + | |
| − | |-
| + | |
| − | | (I)
| + | |
| − | | <math>\ |AB| + |BC| = |AC|</math>
| + | |
| − | | Voraussetzung + Def. Zwischenrelation
| + | |
| − | |-
| + | |
| − | | (II)
| + | |
| − | | <math>\ |AB| = |A'B'|; |BC| = |B'C'|;|AC| = |A'C'|</math>
| + | |
| − | | (I) + Abstandsinvarianz der Bewegung (Def. Bewegung)
| + | |
| − | |-
| + | |
| − | | (III)
| + | |
| − | | <math>\ |A'B'| + |B'C'| = |A'C'|</math>
| + | |
| − | | (I)+(II) Rechnen mit rationalen Zahlen
| + | |
| − | |-
| + | |
| − | | (IV)
| + | |
| − | | <math>\operatorname{Zw}(A', B', C')</math>
| + | |
| − | | (III) + Def. Zwischenrelation
| + | |
| − | |}--[[Benutzer:Tja???|Tja???]] 17:56, 19. Okt. 2010 (UTC)
| + | |
| − | sehr gut, --[[Benutzer:*m.g.*|*m.g.*]] 16:10, 20. Okt. 2010 (UTC)
| + | |
| − | <br />Die Frage mag haarspalterisch sein (sorry), aber warum in Beweisschritt II die Begründung mit (I)? --[[Benutzer:Bagheera|Bagheera]] 12:38, 23. Okt. 2010 (UTC)
| + | |
| − | <br />Die Frage ist nicht haarspalterisch, Sie haben recht, (I) spielt für die Begründung von (II) keine Rolle, war mir gar nicht aufgefallen. --[[Benutzer:*m.g.*|*m.g.*]] 21:08, 25. Okt. 2010 (UTC)
| + | |
Aktuelle Version vom 18. Oktober 2011, 11:36 Uhr
Es seien  drei paarweise verschiedene Punkte mit
drei paarweise verschiedene Punkte mit
(*) 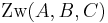 .
.
zu zeigen:
(**) 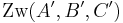
Wir übersetzen zunächst (*):
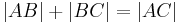
entsprechend (**) haben wir zu zeigen, dass 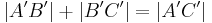 gilt.
gilt.
Den Rest können Sie alleine ... .
 drei paarweise verschiedene Punkte mit
drei paarweise verschiedene Punkte mit
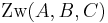 .
.
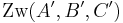
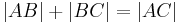
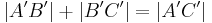 gilt.
gilt.

