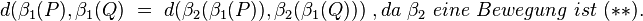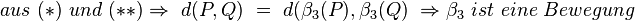Serie 01: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 1.2)
(→‎Aufgabe 1.4)
Zeile 61: Zeile 61:
  
 
<math>\beta_2 \circ  \beta_1</math> ist eine Bewegung.
 
<math>\beta_2 \circ  \beta_1</math> ist eine Bewegung.
 +
 +
 +
<br>
 +
<math> Es\ seien\ M_1,\ M_2\ Mengen, \beta_1,\ \beta_2 \ Bewegungen,\ d () \ sei\ die\ Abstandsfunktion </math><br>
 +
<math> zz.:\ \beta_3 := \beta_2 \circ  \beta_1 \ ist\ eine\ Bewegung,\ also\ d( \beta_3(P),\beta_3(Q)) \ = \ d(P,Q) </math><br>
 +
<math> Beweis:</math><br>
 +
<math> d(P, Q)\ = \ d(\beta_1(P),\beta_1(Q) \ , da \ \beta_1 \ eine\ Bewegung\  ist. \(*)</math> <br>
 +
<math> d(\beta_1(P),\beta_1(Q) \ = \ d( \beta_2( \beta_1 ( P)), \beta_2( \beta_1(Q))) \ , da \ \beta_2 \ eine\ Bewegung\ ist \ (**). </math><br>
 +
<math> aus\ (*) \ und\ (**) \Rightarrow \ d (P,Q) \ = \ d( \beta_3(P), \beta_3(Q) \ \Rightarrow \beta_3 \ ist \ eine \ Bewegung </math><br>

Version vom 19. Oktober 2011, 12:35 Uhr

Inhaltsverzeichnis

Aufgabe 1.1

Definieren Sie für die ebene Geometrie den Begriff Bewegung
(Definition 1.1)

Eine Bewegung ist eine Abbildung der Ebene auf sich, bei der Streckenlängen erhalten bleiben. Pipi Langsocke 12:45, 19. Okt. 2011 (CEST)

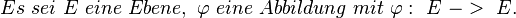
Es \ sei \ E \ eine \ Ebene, \ \varphi \ eine \ Abbildung \ mit \ \varphi : \ E \ -> \ E.
\varphi \ heisst \ Bewegung \ genau \ dann, \ wenn \ \varphi \ laengenerhaltend \ ist.
--Peterpummel 12:46, 19. Okt. 2011 (CEST)

Aufgabe 1.2

Definieren Sie die Begriffe injektiv und surjektiv

injektiv: Es seien eine Ausgangsmenge M und eine Zielmenge N. Injektivität ist dann gegeben, wenn gilt: Jedes Element der Menge M kann einem Element der Zielmenge N eindeutig zugeordnet werden.

surjektiv: Es seien eine Ausgangsmenge M und eine Zielmenge N. Surjektivität ist dann gegeben, wenn gilt: Jedes Element der Zielmenge N besitzt mindestens ein Urbild in der Ausgangsmenge M. Pipi Langsocke 12:48, 19. Okt. 2011 (CEST)

Definieren Sie die Begriffe injektiv und surjektiv

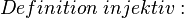
Definition\ injektiv:
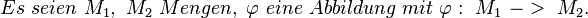
Es\ seien\ M_1,\ M_2\ Mengen,\ \varphi \ eine\ Abbildung\ mit\ \varphi:\ M_1\ ->\ M_2.
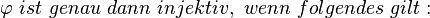
\varphi\ ist\ genau\ dann\ injektiv, \ wenn\ folgendes\ gilt:
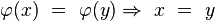
\varphi (x)\ = \ \varphi (y) \Rightarrow \ x\ =\ y


In Worten heisst das nichts anderes als, das wenn ein Element abbgebildet wird es nur ein Urbild hat.
Ein Gegebbeispiel wäre z.b die Normalparabel f(x) = x^2 für diese gilt f(2)= 4 = f(-2), also ist diese nicht injektiv
Betrachtet man nun die eingeschränkte Parabel auf D=R^+ (den rechten Ast) so ist diese injektiv.


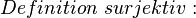
Definition\ surjektiv:
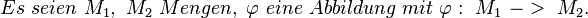
Es\ seien\ M_1,\ M_2\ Mengen,\ \varphi \ eine\ Abbildung\ mit\ \varphi:\ M_1\ ->\ M_2.
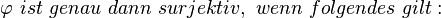
\varphi\ ist\ genau\ dann\ surjektiv, \ wenn\ folgendes\ gilt:
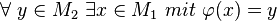
\forall \ y \in M_2 \ \exist x \in M_1\ mit\ \varphi (x) = y
Das heisst nichts anderes als, dass jedes Element in der Bildmenge "getroffen" wird, also zu jedem Element im Bildbereich ein Urbild existiert.
Wieder die Normalparabel: Würden wir hier M_2 = R wählen, dann würden alle negativen Zahlen nicht getroffen werden, also wäre f nicht surjektiv. Eine Einschränkung auf die positiven reellen Zahlen würde zur Surjektivität von f führen.
--Peterpummel 13:14, 19. Okt. 2011 (CEST)

Aufgabe 1.3

Ergänzen Sie die folgende Tabelle
Abbildung Umkehrabbildung
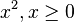x^2, x\ge 0 Wurzel(x) , x \ge 0 (Sorry für die Schreibweise!) -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST)
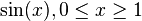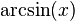\sin (x), 0 \le x \ge 1 \arcsin (x) -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST)
Drehung um Z mit Drehwinkel \alpha Drehung um Z mit dem Drehwinkel 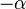- \alpha . -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST)
Spiegelung an der Geraden s bleibt gleich -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST)

Aufgabe 1.4

Beweisen Sie Satz 1.2

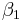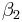Es seien \beta_1 und \beta_2 zwei Bewegungen.

zu zeigen:

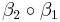\beta_2 \circ \beta_1 ist eine Bewegung.



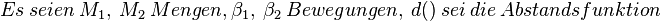
Es\ seien\ M_1,\ M_2\ Mengen, \beta_1,\ \beta_2 \ Bewegungen,\ d () \ sei\ die\ Abstandsfunktion
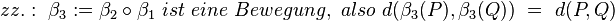
zz.:\ \beta_3 := \beta_2 \circ \beta_1 \ ist\ eine\ Bewegung,\ also\ d( \beta_3(P),\beta_3(Q)) \ = \ d(P,Q)
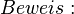
Beweis:
Fehler beim Parsen(Lexikalischer Fehler): d(P, Q)\ = \ d(\beta_1(P),\beta_1(Q) \ , da \ \beta_1 \ eine\ Bewegung\ ist. \(*)

d(\beta_1(P),\beta_1(Q) \ = \ d( \beta_2( \beta_1 ( P)), \beta_2( \beta_1(Q))) \ , da \ \beta_2 \ eine\ Bewegung\ ist \ (**).
aus\ (*) \ und\ (**) \Rightarrow \ d (P,Q) \ = \ d( \beta_3(P), \beta_3(Q) \ \Rightarrow \beta_3 \ ist \ eine \ Bewegung

Von „http://geometrie.zum.de/index.php?title=Serie_01&oldid=8699“