|
|
| Zeile 5: |
Zeile 5: |
| | | | |
| | ::(Definition 1.1) | | ::(Definition 1.1) |
| − | Eine Bewegung ist eine Abbildung der Ebene auf sich, bei der Streckenlängen erhalten bleiben. [[Benutzer:Pipi Langsocke|Pipi Langsocke]] 12:45, 19. Okt. 2011 (CEST)
| |
| − |
| |
| − | <math> Es \ sei \ E \ eine \ Ebene, \ \varphi \ eine \ Abbildung \ mit \ \varphi : \ E \ -> \ E. </math><br>
| |
| − | <math> \varphi \ heisst \ Bewegung \ genau \ dann, \ wenn \ \varphi \ laengenerhaltend \ ist. </math><br>
| |
| − | --[[Benutzer:Peterpummel|Peterpummel]] 12:46, 19. Okt. 2011 (CEST)<br>
| |
| | | | |
| | ===Aufgabe 1.2=== | | ===Aufgabe 1.2=== |
| | ::Definieren Sie die Begriffe ''injektiv'' und ''surjektiv'' | | ::Definieren Sie die Begriffe ''injektiv'' und ''surjektiv'' |
| − |
| |
| − | ''injektiv'': Es seien eine Ausgangsmenge M und eine Zielmenge N. Injektivität ist dann gegeben, wenn gilt: Jedes Element der Menge M kann einem Element der Zielmenge N eindeutig zugeordnet werden.
| |
| − |
| |
| − | ''surjektiv'': Es seien eine Ausgangsmenge M und eine Zielmenge N. Surjektivität ist dann gegeben, wenn gilt: Jedes Element der Zielmenge N besitzt mindestens ein Urbild in der Ausgangsmenge M. [[Benutzer:Pipi Langsocke|Pipi Langsocke]] 12:48, 19. Okt. 2011 (CEST)
| |
| − | <br><br>
| |
| − | ::Definieren Sie die Begriffe ''injektiv'' und ''surjektiv''
| |
| − |
| |
| − | <math> Definition\ injektiv:</math><br>
| |
| − | <math> Es\ seien\ M_1,\ M_2\ Mengen,\ \varphi \ eine\ Abbildung\ mit\ \varphi:\ M_1\ ->\ M_2. </math><br>
| |
| − | <math> \varphi\ ist\ genau\ dann\ injektiv, \ wenn\ folgendes\ gilt:</math><br>
| |
| − | <math> \varphi (x)\ = \ \varphi (y) \Rightarrow \ x\ =\ y </math><br>
| |
| − |
| |
| − |
| |
| − | In Worten heisst das nichts anderes als, das wenn ein Element abbgebildet wird es nur ein Urbild hat.<br>
| |
| − | Ein Gegebbeispiel wäre z.b die Normalparabel f(x) = x^2 für diese gilt f(2)= 4 = f(-2), also ist diese nicht injektiv<br>
| |
| − | Betrachtet man nun die eingeschränkte Parabel auf D=R^+ (den rechten Ast) so ist diese injektiv.
| |
| − |
| |
| − |
| |
| − | <math> Definition\ surjektiv:</math><br>
| |
| − | <math> Es\ seien\ M_1,\ M_2\ Mengen,\ \varphi \ eine\ Abbildung\ mit\ \varphi:\ M_1\ ->\ M_2. </math><br>
| |
| − | <math> \varphi\ ist\ genau\ dann\ surjektiv, \ wenn\ folgendes\ gilt:</math><br>
| |
| − | <math> \forall \ y \in M_2 \ \exist x \in M_1\ mit\ \varphi (x) = y </math><br>
| |
| − | Das heisst nichts anderes als, dass jedes Element in der Bildmenge "getroffen" wird, also zu jedem Element im Bildbereich ein Urbild existiert.<br>
| |
| − | Wieder die Normalparabel: Würden wir hier M_2 = R wählen, dann würden alle negativen Zahlen nicht getroffen werden, also wäre f nicht surjektiv.
| |
| − | Eine Einschränkung auf die positiven reellen Zahlen würde zur Surjektivität von f führen.<br>
| |
| − | --[[Benutzer:Peterpummel|Peterpummel]] 13:14, 19. Okt. 2011 (CEST)
| |
| | | | |
| | ===Aufgabe 1.3=== | | ===Aufgabe 1.3=== |
| Zeile 46: |
Zeile 15: |
| | | Abbildung || Umkehrabbildung | | | Abbildung || Umkehrabbildung |
| | |- | | |- |
| − | | <math>x^2, x\ge 0</math> || Wurzel(x) , x \ge 0 (Sorry für die Schreibweise!) -[[Benutzer:Pipi Langsocke|Pipi Langsocke]] 13:11, 19. Okt. 2011 (CEST) | + | | <math>x^2, x\ge 0</math> || |
| | |- | | |- |
| − | |<math>\sin (x), 0 \le x \ge 1</math> ||<math> \arcsin (x) </math> -[[Benutzer:Pipi Langsocke|Pipi Langsocke]] 13:11, 19. Okt. 2011 (CEST) | + | |<math>\sin (x), 0 \le x \ge 1</math> || |
| | |- | | |- |
| − | |Drehung um Z mit Drehwinkel <math> \alpha </math>|| Drehung um Z mit dem Drehwinkel <math> - \alpha </math>. -[[Benutzer:Pipi Langsocke|Pipi Langsocke]] 13:11, 19. Okt. 2011 (CEST) | + | |Drehung um Z mit Drehwinkel <math> \alpha </math>|| |
| | |- | | |- |
| − | |Spiegelung an der Geraden <math> s </math>|| bleibt gleich -[[Benutzer:Pipi Langsocke|Pipi Langsocke]] 13:11, 19. Okt. 2011 (CEST) | + | |Spiegelung an der Geraden <math> s </math>|| |
| | |} | | |} |
| | | | |
| Zeile 63: |
Zeile 32: |
| | | | |
| | <math>\beta_2 \circ \beta_1</math> ist eine Bewegung. | | <math>\beta_2 \circ \beta_1</math> ist eine Bewegung. |
| − |
| |
| − |
| |
| − | <br>
| |
| − | <math> Es\ seien\ M_1,\ M_2,\ M_3\ Ebenen, P,Q \in M_1\ .</math><br>
| |
| − | <math> \beta_1,\ \beta_2 \ mit \ \beta1 : M_1 ->M_2 \ und \ \beta_2 : M_2 -> M_3 \ Bewegungen,\ d () \ sei\ die\ Abstandsfunktion </math><br>
| |
| − | <math> zz.:\ \beta_3 := \beta_2 \circ \beta_1 \ ist\ eine\ Bewegung,\ also\ d( \beta_3(P),\beta_3(Q)) \ = \ d(P,Q) </math><br><br>
| |
| − | <math> Beweis:</math><br><br>
| |
| − | <math> Es\ gilt\ nach\ Voraussetzung:</math><br>
| |
| − | <math> d(P, Q)\ = \ d(\beta_1(P),\beta_1(Q)) \ , da \ \beta_1 \ eine\ Bewegung\ ist. \(*)</math> <br>
| |
| − | <math> d(\beta_1(P),\beta_1(Q) \ = \ d( \beta_2( \beta_1 ( P)), \beta_2( \beta_1(Q))) \ , da \ \beta_2 \ eine\ Bewegung\ ist \ (**). </math><br>
| |
| − | <math> aus\ (*) \ und\ (**) \Rightarrow \ d (P,Q) \ = \ d( \beta_3(P), \beta_3(Q) \ \Rightarrow \beta_3 \ ist \ eine \ Bewegung </math><br>
| |
| − | --[[Benutzer:Peterpummel|Peterpummel]] 13:35, 19. Okt. 2011 (CEST)
| |
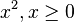
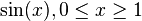


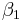 und
und 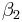 zwei Bewegungen.
zwei Bewegungen.
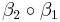 ist eine Bewegung.
ist eine Bewegung.

