Lösung von Aufgabe 1.3 2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Es seien <math>\beta_1</math> und <math>\beta_2</math> zwei Bewegungen. zu zeigen: <math>\beta_2 \circ \beta_1</math> ist eine Bewegung.“) |
HecklF (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
zu zeigen: | zu zeigen: | ||
| − | <math>\beta_2 \circ \beta_1</math> ist eine Bewegung. | + | <math>\beta_2 \circ \beta_1</math> ist eine Bewegung. <br /> |
| + | |||
| + | Nach Definiton ist eine Bewegung eine Abbildung der Ebene auf sich mit speziellen Eigenschaften, die jetzt aber egal sind. Demzufolge existiert eine Ebene (die existiert nach den Inzidenzaxiomen sowieso). | ||
| + | <br /><br /> | ||
| + | <math>\epsilon \rightarrow \beta_1(\epsilon_1 )</math> nach Voraussetzung | ||
| + | <br /><br /> | ||
| + | <math>\epsilon_1 \rightarrow \beta_2(\epsilon_2 )</math> Voraussetzung und vorheriger Ausführung. | ||
| + | <br /><br /> | ||
| + | Da es für jede Nacheinanderausführung (bzw. für jede Gruppe) ein Einselement gibt, folgt hier eindeutig, dass auch <math>\epsilon \rightarrow \epsilon_2</math> eine Bewegung ist. --[[Benutzer:HecklF|Flo60]] 21:42, 24. Okt. 2011 (CEST) | ||
Aktuelle Version vom 24. Oktober 2011, 20:42 Uhr
Es seien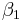 
und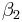 
zwei Bewegungen.
zu zeigen:
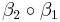ist eine Bewegung.
Nach Definiton ist eine Bewegung eine Abbildung der Ebene auf sich mit speziellen Eigenschaften, die jetzt aber egal sind. Demzufolge existiert eine Ebene (die existiert nach den Inzidenzaxiomen sowieso).
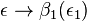nach Voraussetzung
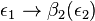Voraussetzung und vorheriger Ausführung.
Da es für jede Nacheinanderausführung (bzw. für jede Gruppe) ein Einselement gibt, folgt hier eindeutig, dass auch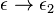 
eine Bewegung ist. --Flo60 21:42, 24. Okt. 2011 (CEST)
