Lösung Serie 02: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „==Aufgabe 2.1== Erstellen Sie eine Konstruktionsvorschrift zur Konstruktion des Bildes eine Punktes <math>P</math> bei der Spiegelung an der Geraden <math>g</math…“) |
HecklF (Diskussion | Beiträge) (→Aufgabe 2.5) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
==Aufgabe 2.3== | ==Aufgabe 2.3== | ||
| − | Definieren Sie den Begriff Geradenspiegelung. (Skript: http://wikis.zum.de/geowiki/Geradenspiegelungen_(2011/12)#Definition_2.1:_.28Spiegelung_an_der_Geraden_.29) | + | Definieren Sie den Begriff Geradenspiegelung. (Skript: http://wikis.zum.de/geowiki/Geradenspiegelungen_(2011/12)#Definition_2.1:_.28Spiegelung_an_der_Geraden_.29)<br /> |
| + | ::Es sei <math>\ g</math> eine Gerade. Unter der Spiegelung <math>\ S_g</math> an der Geraden <math>g</math>versteht man eine Abbildung der Ebene auf sich, bei der die Gerade g auf sich abgebildet wird und der Punkt P so abgebildet wird, dass gilt: <math>\overline{P\rho(P) } \perp g</math> und <math>|Pg| = |g\rho (P)|</math>. | ||
| + | |||
| + | Zweite Möglichkeit (etwas einfacher und plausibler ausgedrückt): | ||
| + | |||
| + | ::Es sei <math>\ g</math> eine Gerade. Unter der Spiegelung <math>\ S_g</math> an der Geraden <math>g</math>versteht man eine Abbildung der Ebene auf sich, bei der die Gerade g auf sich abgebildet wird und Mittelsenkrechte der Strecke <math>\overline{P\rho(P) }</math> ist. | ||
| + | <br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 20:29, 31. Okt. 2011 (CET) | ||
==Aufgabe 2.4== | ==Aufgabe 2.4== | ||
| Zeile 19: | Zeile 26: | ||
Beweisen Sie: :: Eine Geradenspiegelung <math>\ S</math> ist durch die Angabe eines Punktes <math>\ P</math> und dem Bild von <math>\ S(P)</math> eindeutig bestimmt, falls <math>\ P \not= S(P)</math> gilt. | Beweisen Sie: :: Eine Geradenspiegelung <math>\ S</math> ist durch die Angabe eines Punktes <math>\ P</math> und dem Bild von <math>\ S(P)</math> eindeutig bestimmt, falls <math>\ P \not= S(P)</math> gilt. | ||
(Satz 2.3 aus dem Skript) | (Satz 2.3 aus dem Skript) | ||
| + | <br /> | ||
| + | Nach zu Grunde legen der Definition des Bildes eines Punktes bei einer Geradenspiegelung geht dieses unmittelbar aus dem Winkelkonstruktionsaxiom hervor und der Eindeutigkeit des Mittelpunktes. --[[Benutzer:HecklF|Flo60]] 21:31, 31. Okt. 2011 (CET) | ||
[[Kategorie:Elementargeometrie]] | [[Kategorie:Elementargeometrie]] | ||
Aktuelle Version vom 31. Oktober 2011, 21:36 Uhr
Inhaltsverzeichnis |
Aufgabe 2.1
Erstellen Sie eine Konstruktionsvorschrift zur Konstruktion des Bildes eine Punktes 
bei der Spiegelung an der Geraden 
für den Fall, dass außerhalb von liegt. Begründen Sie die Korrektheit eines jeden Konstruktionsschrittes. (s. Skript: http://wikis.zum.de/geowiki/Geradenspiegelungen_(2011/12)#.C3.9Cbungsaufgabe:)
Ich hoffe, dass das alles so stimmt ;-)
Datei:Konstruktion Sg(P).zip
--Flo60 00:00, 31. Okt. 2011 (CET)
Aufgabe 2.2
Inwiefern ist die Konstruktionsvorschrift aus Aufgabe 01 eine Definition?
Aufgabe 2.3
Definieren Sie den Begriff Geradenspiegelung. (Skript: http://wikis.zum.de/geowiki/Geradenspiegelungen_(2011/12)#Definition_2.1:_.28Spiegelung_an_der_Geraden_.29)
- Es sei
eine Gerade. Unter der Spiegelung 
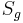an der Geraden versteht man eine Abbildung der Ebene auf sich, bei der die Gerade g auf sich abgebildet wird und der Punkt P so abgebildet wird, dass gilt: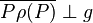 
und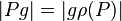 
.
- Es sei
Zweite Möglichkeit (etwas einfacher und plausibler ausgedrückt):
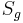- Es sei eine Gerade. Unter der Spiegelung an der Geraden versteht man eine Abbildung der Ebene auf sich, bei der die Gerade g auf sich abgebildet wird und Mittelsenkrechte der Strecke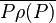
ist.
- Es sei
--Flo60 20:29, 31. Okt. 2011 (CET)
Aufgabe 2.4
Beweisen Sie: Jede Geradenspiegelung ist abstandserhaltend. (Satz 2.1 aus dem Skript)
Aufgabe 2.5
Beweisen Sie: :: Eine Geradenspiegelung 
ist durch die Angabe eines Punktes 
und dem Bild von 
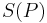eindeutig bestimmt, falls 
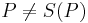gilt.
(Satz 2.3 aus dem Skript)
Nach zu Grunde legen der Definition des Bildes eines Punktes bei einer Geradenspiegelung geht dieses unmittelbar aus dem Winkelkonstruktionsaxiom hervor und der Eindeutigkeit des Mittelpunktes. --Flo60 21:31, 31. Okt. 2011 (CET)
