Serie 01: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 1.3)
(→‎Aufgabe 1.3)
 
(22 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
[[Lösungen zu den Aufgaben]]
 +
<br />
 +
<br />
 +
Hi Leute,<br/>
 +
keine Panik, ich habe eure Lösungen in die neue Seite gepackt - genau so, wie ihr sie bearbeitet habt. Ich glaub es ist besser so, da die Aufgaben für alle jederzeit bearbeitbar sind. Zumindest hat sich das System letztes Jahr in der Geometrieeinführung bewährt. --[[Benutzer:HecklF|Flo60]] 20:36, 19. Okt. 2011 (CEST)
 +
 
===Aufgabe 1.1===
 
===Aufgabe 1.1===
 
:: Definieren Sie für die ebene Geometrie den Begriff ''Bewegung''
 
:: Definieren Sie für die ebene Geometrie den Begriff ''Bewegung''
Zeile 13: Zeile 19:
 
| Abbildung || Umkehrabbildung
 
| Abbildung || Umkehrabbildung
 
|-  
 
|-  
−
| <math>x^2, x\ge 0</math> || ...
+
| <math>x^2, x\ge 0</math> ||  
 
|-
 
|-
−
|<math>\sin (x), 0 \le x \ge ...</math> ||<math> \arcsin (x) </math>
+
|<math>\sin (x), -\frac{\pi}{2} \le x \le \frac{\pi}{2}</math>||
 
|-
 
|-
−
|Drehung um Z mit Drehwinkel <math> \alpha </math>|| ...
+
|Drehung um Z mit Drehwinkel <math> \alpha </math>||  
 +
|-
 +
|Spiegelung an der Geraden <math> s </math>||
 
|}
 
|}
 +
Ich habe ein Problem mit der Aufgabenstellung in der zweiten Zeile. Müsste es nicht heißen <math>0 \le x \le \pi</math> ?<br />
 +
--[[Benutzer:Sternchen|Sternchen]] 20:45, 26. Okt. 2011 (CEST)<br />
 +
OK, also  <math>-\frac{\pi}{2} \le x \le \frac{\pi}{2}</math> beim Arkussinus und <math>0 \le x \le \pi</math> beim Arkuskosinus, alles klar.<br />
 +
--[[Benutzer:Sternchen|Sternchen]] 11:59, 27. Okt. 2011 (CEST)<br /><br />
 +
Sie haben völlig Recht. Beim Schreiben der Aufgabe war ich in Gedanken wohl beim Wertebereich der Funktion <math>\sin (x)</math>.--[[Benutzer:*m.g.*|*m.g.*]] 13:39, 3. Nov. 2011 (CET)
 +
 +
===Aufgabe 1.4===
 +
::Beweisen Sie Satz 1.2
 +
 +
Es seien <math>\beta_1</math> und <math>\beta_2</math> zwei Bewegungen.
 +
 +
zu zeigen:
 +
 +
<math>\beta_2 \circ  \beta_1</math> ist eine Bewegung.

Aktuelle Version vom 3. November 2011, 13:40 Uhr

Lösungen zu den Aufgaben

Hi Leute,
keine Panik, ich habe eure Lösungen in die neue Seite gepackt - genau so, wie ihr sie bearbeitet habt. Ich glaub es ist besser so, da die Aufgaben für alle jederzeit bearbeitbar sind. Zumindest hat sich das System letztes Jahr in der Geometrieeinführung bewährt. --Flo60 20:36, 19. Okt. 2011 (CEST)

Inhaltsverzeichnis

Aufgabe 1.1

Definieren Sie für die ebene Geometrie den Begriff Bewegung
(Definition 1.1)

Aufgabe 1.2

Definieren Sie die Begriffe injektiv und surjektiv

Aufgabe 1.3

Ergänzen Sie die folgende Tabelle
Abbildung Umkehrabbildung
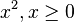x^2, x\ge 0
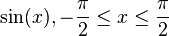\sin (x), -\frac{\pi}{2} \le x \le \frac{\pi}{2}
Drehung um Z mit Drehwinkel \alpha
Spiegelung an der Geraden s

Ich habe ein Problem mit der Aufgabenstellung in der zweiten Zeile. Müsste es nicht heißen 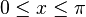0 \le x \le \pi ?
--Sternchen 20:45, 26. Okt. 2011 (CEST)
OK, also 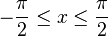-\frac{\pi}{2} \le x \le \frac{\pi}{2} beim Arkussinus und 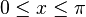0 \le x \le \pi beim Arkuskosinus, alles klar.
--Sternchen 11:59, 27. Okt. 2011 (CEST)

Sie haben völlig Recht. Beim Schreiben der Aufgabe war ich in Gedanken wohl beim Wertebereich der Funktion 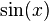\sin (x).--*m.g.* 13:39, 3. Nov. 2011 (CET)

Aufgabe 1.4

Beweisen Sie Satz 1.2

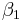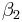Es seien \beta_1 und \beta_2 zwei Bewegungen.

zu zeigen:

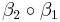\beta_2 \circ \beta_1 ist eine Bewegung.

Von „http://geometrie.zum.de/index.php?title=Serie_01&oldid=9146“