Serie 03: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „==Aufgabe 3.1== Beweisen Sie: wenn eine Bewegung <math>\varphi</math> zwei verschiedene Fixpunkte <math>A</math> und <math>B</math> hat, dann hat“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 3.1) |
||
| Zeile 1: | Zeile 1: | ||
| + | ==Aufgabe == | ||
| + | (alles in ein und derselben Ebene) | ||
| + | Es sei <math>k</math> ein Kreis mit dem Mittelpunkt <math>M</math> und dem Radius <math>r</math>. Ferner sei <math>g</math> eine Gerade, die durch den Mittelpunkt von k geht. Schließlich sei <math>Z</math> der gemeinsame Schnittpunkt der Senkrechten in <math>M</math> auf <math>g</math> mit <math>k</math>. Wir definieren eine Abbildung <math>\varphi</math> von <math>k\setminus_Z</math> auf <math>g</math>: <math>\forall P \in k\setminus_Z: \varphi(P)=ZP \cap g</math> | ||
| + | |||
==Aufgabe 3.1== | ==Aufgabe 3.1== | ||
| − | Beweisen Sie: wenn eine Bewegung <math>\varphi</math> zwei verschiedene Fixpunkte <math>A</math> und <math>B</math> hat, dann hat | + | Beweisen Sie: wenn eine Bewegung <math>\varphi</math> zwei verschiedene Fixpunkte <math>A</math> und <math>B</math> hat, dann hat ist die Gerade <math>AB</math> eine Fixpunktgerade bezüglich <math>\varphi</math>. |
| + | ==Aufgabe 3.2== | ||
| + | Beweisen Sie: Wenn drei nicht kollineare Punkte <math>A,B,C</math> Fixpunkte der Bewegung <math>\varphi</math> sind, so ist <math>\varphi</math> die identische Abbildung. | ||
| + | == | ||
Version vom 8. November 2011, 12:45 Uhr
Aufgabe
(alles in ein und derselben Ebene)
Es sei 
ein Kreis mit dem Mittelpunkt 
und dem Radius 
. Ferner sei 
eine Gerade, die durch den Mittelpunkt von k geht. Schließlich sei 
der gemeinsame Schnittpunkt der Senkrechten in auf mit . Wir definieren eine Abbildung 
von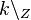 
auf : 
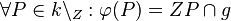
Aufgabe 3.1
Beweisen Sie: wenn eine Bewegung zwei verschiedene Fixpunkte 
und 
hat, dann hat ist die Gerade 
eine Fixpunktgerade bezüglich .
Aufgabe 3.2
Beweisen Sie: Wenn drei nicht kollineare Punkte 
Fixpunkte der Bewegung sind, so ist die identische Abbildung.
==
