Serie 04: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgabe 4.1= Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: …“) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.1) |
||
| Zeile 1: | Zeile 1: | ||
=Aufgabe 4.1= | =Aufgabe 4.1= | ||
| − | Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild bei <math>\beta</math> eindeutig bestimmt. | + | Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild <math>P'</math> bei <math>\beta</math> eindeutig bestimmt. |
[[Kategorie:Elementargeometrie]] | [[Kategorie:Elementargeometrie]] | ||
Version vom 15. November 2011, 12:42 Uhr
Aufgabe 4.1
Es seien 
drei nichtkollineare Punkte und 
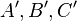ihre Bilder bei der Bewegung 
. Man beweise: Für jeden Punkt 
ist jetzt sein Bild 
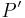bei eindeutig bestimmt.
