Serie 04: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.1) |
||
| Zeile 1: | Zeile 1: | ||
=Aufgabe 4.1= | =Aufgabe 4.1= | ||
Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild <math>P'</math> bei <math>\beta</math> eindeutig bestimmt. | Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild <math>P'</math> bei <math>\beta</math> eindeutig bestimmt. | ||
| + | =Aufgabe 4.2= | ||
| + | Es seien <math>a</math> und <math>b</math> zwei Geraden, die sich in genau dem Punkt <math>Z</math> schneiden. Man beweise: | ||
| + | Die Nacheinanderausführung <math>S_b \circ S_a</math> ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden <math>a</math> und <math>b</math>. | ||
[[Kategorie:Elementargeometrie]] | [[Kategorie:Elementargeometrie]] | ||
Version vom 15. November 2011, 12:48 Uhr
Aufgabe 4.1
Es seien  drei nichtkollineare Punkte und
drei nichtkollineare Punkte und 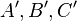 ihre Bilder bei der Bewegung
ihre Bilder bei der Bewegung  . Man beweise: Für jeden Punkt
. Man beweise: Für jeden Punkt  ist jetzt sein Bild
ist jetzt sein Bild 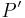 bei
bei  eindeutig bestimmt.
eindeutig bestimmt.
Aufgabe 4.2
Es seien  und
und  zwei Geraden, die sich in genau dem Punkt
zwei Geraden, die sich in genau dem Punkt  schneiden. Man beweise:
Die Nacheinanderausführung
schneiden. Man beweise:
Die Nacheinanderausführung 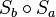 ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden
ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden  und
und  .
.

