Zu den Lösungen Serie 04 WiSe 2011/12: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „=Aufgabe 4.1= Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: …“) |
HecklF (Diskussion | Beiträge) (→Aufgabe 4.1) |
||
| Zeile 1: | Zeile 1: | ||
=Aufgabe 4.1= | =Aufgabe 4.1= | ||
Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild <math>P'</math> bei <math>\beta</math> eindeutig bestimmt. | Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild <math>P'</math> bei <math>\beta</math> eindeutig bestimmt. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | Voraussetzung: nkoll(A,B,C) sowie A', B' und C' und P | ||
| + | Behauptung: <math>\beta (P)</math> = P' ist eindeutig bestimmt für jede Abbildung. | ||
| + | <br /> | ||
| + | Es sind nun verschiedene Fälle zu betrachten. Der einfachste Fall ist, dass alle Punkte Fixpunkte sind, dann haben wir - nach dem vorherigen Satz gezeigt - die Identität. In diesem Fall spielt es keine Rolle, ob <math>P \equiv A \vee P \equiv B \vee P \equiv C</math> oder ob P verschieden von A, B oder C ist. In diesen Fällen sind wir fertig.<br /> | ||
| + | |||
| + | Nun Fall II: Bewegung ist nicht die Identität (hier spielt es übrigens schon eine Rolle, ob P verschieden ist von A, B oder C oder nicht. Da die Voraussetzung nicht erfüllt werden kann, wenn P nicht verschieden ist von den drei nichtkollinearen Punkten (kann durch eine Mittelsenkrechte ganz leicht gezeigt werden) nehmen wir an, dass dem nicht der Fall ist, also P ungleich A, B, C. | ||
| + | |||
| + | Bei der Bewegung bleiben die Abstände erhalten. <math>\\left| AB \right| </math> = <math>\left| A'B' \right|</math> . Weiter bleibt nun <math>\left| AP \right| = \left| A'P' \right| und \left| PB \right| = \left| P'B' \right|</math>. | ||
| + | Nun kann P (und somit auch später P') in zwei Halbebenen bzgl. AB liegen oder auf AB selbst. Wenn P aber auf AB liegt, sind wir fertig, denn dann ergibt sich nur eine Möglichkeit wegen der Zwischenrelation. | ||
| + | Da nun aber zusätzlich gelten muss, dass <math>\left| PC \right| = \left| P'C' \right|</math> ist nun folgendes unmittelbar einleuchtend und ersichtlich:<br /> | ||
| + | Wenn P und C bzgl. AB in verschiedenen Halbebenen liegen, liegen auch P' und C' in verschiedenen Halbebenen bzgl. AB. Wenn P und C bzgl. AB in ein und derselben Halbebene liegen, liegen auch P' und C' in ein und derselben Halbebene bzgl. AB. Demnach ist P' eindeutig.<br /><br /> | ||
| + | Ich werde das ganze evtl. nochmal schöner schreiben, da es vielleicht verwirrend ist. Wenn mein Geogebra wieder funktioniert, schicke ich eine Applikation nach. --[[Benutzer:HecklF|Flo60]] 20:21, 15. Nov. 2011 (CET) | ||
| + | |||
=Aufgabe 4.2= | =Aufgabe 4.2= | ||
Es seien <math>a</math> und <math>b</math> zwei Geraden, die sich in genau dem Punkt <math>Z</math> schneiden. Man beweise: | Es seien <math>a</math> und <math>b</math> zwei Geraden, die sich in genau dem Punkt <math>Z</math> schneiden. Man beweise: | ||
Version vom 15. November 2011, 21:21 Uhr
Inhaltsverzeichnis[Verbergen] |
Aufgabe 4.1
Es seien  drei nichtkollineare Punkte und
drei nichtkollineare Punkte und 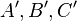 ihre Bilder bei der Bewegung
ihre Bilder bei der Bewegung  . Man beweise: Für jeden Punkt
. Man beweise: Für jeden Punkt  ist jetzt sein Bild
ist jetzt sein Bild 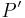 bei
bei  eindeutig bestimmt.
eindeutig bestimmt.
Voraussetzung: nkoll(A,B,C) sowie A', B' und C' und P
Behauptung: 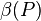 = P' ist eindeutig bestimmt für jede Abbildung.
= P' ist eindeutig bestimmt für jede Abbildung.
Es sind nun verschiedene Fälle zu betrachten. Der einfachste Fall ist, dass alle Punkte Fixpunkte sind, dann haben wir - nach dem vorherigen Satz gezeigt - die Identität. In diesem Fall spielt es keine Rolle, ob 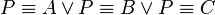 oder ob P verschieden von A, B oder C ist. In diesen Fällen sind wir fertig.
oder ob P verschieden von A, B oder C ist. In diesen Fällen sind wir fertig.
Nun Fall II: Bewegung ist nicht die Identität (hier spielt es übrigens schon eine Rolle, ob P verschieden ist von A, B oder C oder nicht. Da die Voraussetzung nicht erfüllt werden kann, wenn P nicht verschieden ist von den drei nichtkollinearen Punkten (kann durch eine Mittelsenkrechte ganz leicht gezeigt werden) nehmen wir an, dass dem nicht der Fall ist, also P ungleich A, B, C.
Bei der Bewegung bleiben die Abstände erhalten. Fehler beim Parsen(Syntaxfehler): \\left| AB \right|
=. Weiter bleibt nun
.
Nun kann P (und somit auch später P') in zwei Halbebenen bzgl. AB liegen oder auf AB selbst. Wenn P aber auf AB liegt, sind wir fertig, denn dann ergibt sich nur eine Möglichkeit wegen der Zwischenrelation.
Da nun aber zusätzlich gelten muss, dass 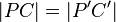 ist nun folgendes unmittelbar einleuchtend und ersichtlich:
ist nun folgendes unmittelbar einleuchtend und ersichtlich:
Wenn P und C bzgl. AB in verschiedenen Halbebenen liegen, liegen auch P' und C' in verschiedenen Halbebenen bzgl. AB. Wenn P und C bzgl. AB in ein und derselben Halbebene liegen, liegen auch P' und C' in ein und derselben Halbebene bzgl. AB. Demnach ist P' eindeutig.
Ich werde das ganze evtl. nochmal schöner schreiben, da es vielleicht verwirrend ist. Wenn mein Geogebra wieder funktioniert, schicke ich eine Applikation nach. --Flo60 20:21, 15. Nov. 2011 (CET)
Aufgabe 4.2
Es seien  und
und  zwei Geraden, die sich in genau dem Punkt
zwei Geraden, die sich in genau dem Punkt  schneiden. Man beweise:
Die Nacheinanderausführung
schneiden. Man beweise:
Die Nacheinanderausführung 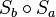 ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden
ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden  und
und  .
.
Aufgabe 4.3
Sie haben mit Ihren Schülern den begriff der Drehung erarbeitet. Jetzt steht eine Erstfestigung an. Entwickeln Sie Fragestellungen, die sich auf die folgende Geogebra-Applikation beziehen und der Festigung des Begriffs der Drehung dienen. Beispiele:
- Der Punkt
 wird bei einer Drehung um
wird bei einer Drehung um  auf den Punkt
auf den Punkt  abgebildet. Wie groß ist der Drehwinkel dabei?
abgebildet. Wie groß ist der Drehwinkel dabei?
- Ist es möglich, dass bei einer Drehung um
 der Punkt
der Punkt 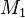 auf den Punkt
auf den Punkt  abgebildet wird?
abgebildet wird?
Aufgabe 4.4
Sowohl die Punkte 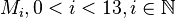 als auch die Punkte
als auch die Punkte 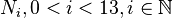 sind zueinander Bilder bei Drehungen um das Zentrum
sind zueinander Bilder bei Drehungen um das Zentrum 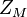 bzw.
bzw. 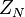 . Berechnen Sie die Koordinaten dieser Drehzentren.
. Berechnen Sie die Koordinaten dieser Drehzentren.

