Serie 04: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4.1) |
(→Aufgabe 4.3) |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | [[Zu den Lösungen Serie 04 WiSe 2011/12]] | ||
=Aufgabe 4.1= | =Aufgabe 4.1= | ||
Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild <math>P'</math> bei <math>\beta</math> eindeutig bestimmt. | Es seien <math>A, B, C</math> drei nichtkollineare Punkte und <math>A', B', C'</math> ihre Bilder bei der Bewegung <math>\beta</math>. Man beweise: Für jeden Punkt <math>P</math> ist jetzt sein Bild <math>P'</math> bei <math>\beta</math> eindeutig bestimmt. | ||
| Zeile 5: | Zeile 6: | ||
Die Nacheinanderausführung <math>S_b \circ S_a</math> ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden <math>a</math> und <math>b</math>. | Die Nacheinanderausführung <math>S_b \circ S_a</math> ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden <math>a</math> und <math>b</math>. | ||
| + | =Aufgabe 4.3= | ||
| + | Sie haben mit Ihren Schülern den Begriff der Drehung erarbeitet. Jetzt steht eine Erstfestigung an. Entwickeln Sie Fragestellungen, die sich auf die folgende Geogebra-Applikation beziehen und der Festigung des Begriffs der Drehung dienen. | ||
| + | Beispiele: | ||
| + | |||
| + | # Der Punkt <math>A</math> wird bei einer Drehung um <math>Z</math> auf den Punkt <math>B</math> abgebildet. Wie groß ist der Drehwinkel dabei? | ||
| + | # Ist es möglich, dass bei einer Drehung um <math>Z</math> der Punkt <math>M_1</math> auf den Punkt <math>M_2</math> abgebildet wird? | ||
| + | |||
| + | <ggb_applet width="771" height="802" version="4.0" ggbBase64="UEsDBBQACAAIAO91bz8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAO91bz8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Z3dcqNIlseve54iQxd7sWHJ5BcJva6ecH3aVSq5Y6q3Y3Y2NjaQhGTKEmgEctm9s++08wr7APNMk0kCEpBIpGwLpOqOqgahFGSe/8mT50cm1MUfH+YzcO8uQy/wX3Vgz+gA1x8FY8+fvuqsoknX6vzxpz9cTN1g6g6XDpgEy7kTveoQUdIbv+oMydie2GPcnQwZ7JLxaNR1hiPWHU/gZGJb9pCNcQeAh9D70Q8GztwNF87I/TK6dedOPxg5UXzh2yha/Hh+/u3bt156qV6wnJ5Pp8PeQzjuAF5NP3zVSXZ+5KfL/egbjosjw4Dnf/7cl6fven4YOf7I7QDRhJX30x9+uPjm+ePgG/jmjaPbVx3G7A64db3pLW+Thc0OOBeFFtwgC3cUefduyH+68TFuczRfdOJiji++/0HugVnWnA4Ye/fe2F2+6hg9aEFeLcTPbjODMNoBwdJz/SgpC5Nrnqdnu7j33G/ytGIvviLpgCgIZkNHnBH87W8AGcgAZ2ID5QbxjWnKrwx5zMByg+SGyA2VZYj8OZFFiSxDZBnCFbv3Qm84c191Js4s5Bb0/MmSq5d9DqPHmRvXJzmwbj08420Kvd94YWxwN5Em58cN40z8NflfIr44zzcSblw1Wq40L5pekjFY/5LoSQ3F6TUhUVwT0YpmmlsuKttdp52QbpiWXyr+E/8tXRFva2bxivLz0y5okoM08eI87SoXSe8A4a0om3hP5M5D0V+wDagt3B4CyvuGybiXUwBtvmEI8N4AIAWE8o/QAqbYMoAZ/4IADCwgykEM4s5BLf4/wuKTmYDyk4mjjPdJAPmFCKAYwLhPEcB7Eoj7Je+jCPMSlALKfyQuD5E4BTYBMfknbAHC6yi6JIO8IOY/5J/55RHAEGDxY8gAMoEpzgeJ6OqmJarOT4mAaQATihPyXs17tOzNvLwFsGhNGtY8f7GKciYazcfpbhQsMi14aR6P1lFPxqdcUPzhYuYM3RkfJ74IJQG4d2aiR8QXmgR+BFIRTXlsunQWt94o/OJGEf9VCL46907fidyH97x0mF47LjsK/PDnZRC9CWaruR8CMApmRlbnYAY39lFWa/4Bb3xBNr+gG1+YG/tMed2AfwNWocuvHyzDtLgzHl+LEuvQwC15488eXy9d524RePlmXJzHQ86FuxrNvLHn+L9yZxVXEXYB6xEIrkcg0zTTigTL8ZfHkHswePiLuwy4aU3YswxGbZPYpm0T1gGPyTcE9fhIa2OIDMawZfGajRzR9QjrWSY0kWUTQgzEeLd8rPiKyQu795k+zoO7bup0Kfr1xofr8HUwWx+KW//GWUSrZZw68NC4FG269KczN/aQONjycXl0NwwevkjXwPJcvzwu+CdD1mA4ja0OeGRAlA+W02Q7lNu4jKhaVsqIyxhxCSP1NW+cfQ9tFJeIt0O5jUtx55VVS5oK02ZCI72MF8bxzOgkvSaNVcL1xTC/8r2on36IvNFd0lQofzBYzYdu5kD5c8LnOufFecHDLu7cpe/OEofmYq6CVSj754avj92RN+cf5ReJSRwh17/zCsijY3e6dNOKz+K0TBos/tbY9NXS4fhU75fB/Nq//4X7QqECF+dpLS/C0dJbCJ8DQz4I3Llrrxp7ocPHkPHm70QP5E0fibGCmycSpuF9cxXdBss48+IhhW9Fx5u5c55ngSh2r7g+mZn/8fc4g+N1WqXV7iUVD2cicwNzz4+FnzsPvGP2eP4GLYoNBplNLR5RnWHIo1PEU1luIn+dyspYkfZuJPLkB5EIiZ1HMYyJnYn3sNFMXnPvN66UqMbaU4TYIBh+5SE3G5Vl5ddl+NeFfgCNtCcAZ7a4deIMNPF355G3a1Oj+Hyfg3FiAljsFxEP2Hc8Kw3jzhsl3TTeufLGY9fPfuMsR6JPJ6NA5gLcw2KdeCBbxCaGjFCMbEQhD2F8h3dsPqi4sj/IC/CdBa9qHEY2fFyKWZI1DjyZZf7S2d9yRhZj1pYzalquosFwe+tyIw/vRKHwlNRR4u1vkskklIiWbhh582ih91Wby1/N3aU3ygyyLHYDmnWDTSPmY9RGvavM+AT3q2FEQ2XEzUaPgvnc8cfAjzPON95yxPv+OgVyDOEqwIHCALIdqyj9YiRPlpyiZEEefzbsN9rhcJqm0vS3fXoqTzVc/57XlGc2nMuNhPofjdTl0iMP3Dpd6Y0wOfQb3PBHLtLSewCXafnLtNQlT8m6iMa7ODnrJUlPdkmTPVmbv/qyAaEc5ESG6U280XZBf447fV7PUUnIy/+G26XMxw5RfIfjq8MHRDJNibdtCCH0mUNI3vg3Sz7UTgPfmfW5+xVUEEaM+9XDJU90SpI42wUR/pwZ29mlxsv2rbU5u7BgzyxG7tX/Ch7vzRczb+RFe4SwzNiwZOixThAbN2vp9kYxRMpBjD5XEPtTEPFUtUpSnqACB4lhqhTWtILakxOiZ+lCTUakbfFoohGPJr/Ho13xqCoaTXWi0fT3aNRANLr2I3cZ8iYUNJ1KTSclTd+mkeqdXpr1dt80S9xUnsrNUG6eLy7JLvXstJVv+bs2tvy5Gq4RkTPPKTvVrUY8vm1NPDaKXtSFh4/IynRiIg1N6L/+///JfOKyPAb+i7MIwn/TGQmTX7TH/sxg0DCZBaFlUsJMKUfpOI3VwT2KKcXYNqiNEcPMapNWGNYQa1fIVcm1O/o0JxhJ8pnCYabW69ByVY2Nt0kY29Qkp9ZnvaHxs0qiGun63uPDzWQSupHMKWEsASL1JEQ9C1kEMYi4eCa07IoeR2IFFYefb6ypUieNUrFGtyVtBnraDBrUBklpUD1pSA8RZBLDtBiENrKqgqGplsZ8Rml+DmaPPAsoCPM5Hf8H8Y4yzv3q8XOO7pKCTialmO2Nf8Wz4OluBeXlU4Wyk+4bPrTv81IYqy82pRuDVCd8VueYoTsVn9a3zaoG56fWd+9wn6ZHqGfk/5PBQXH4ReJ77F8zcds0ixhe4JcnRu9cdyFmpG/8X5aOH4oVb7LM7smoohaTnUHjkDpk9w2yPPXFbhw0YOtpq2y9aWqV03ePy/R17lwm6auRZa/lW5evdUbc1+24dUl6GBsQMYMnOQhBmySxjNi5/8wXoOhYmFnZ1NkA+mt8y+k/L8/A6/9SJJ9IL/lEjSU4tlaCg3pYsBzFNkM2z3UISu9kmIZpGpBBxmwLGfTlc88qhQa1FBroKTRoUKHE63E9hXCPmZbN/1DbNClFUCkQfPkEtEqfyxrqXMpEqh5wF2ZdCj/d667fs04rtyKeVeEASnEAJThQtrwKDlAODrLSEhKSjyhBhTr3uCpwAX0PuFDtqgetdy5dRT0kHkkwDWIjamCI33WhqSQJGUm6+Khyqh3okDlwixQpAYTZs3LBBJ+M/acvhdF7W79EEqiCMOx0DqKgjXlE4tQAjtc1gOONzqj95rDZ1dYMlxbj22N55MYHRQ6US5len4E3KuTAesiBm7vfjbTudyty10cFiTRJHHUEGugJNGhQID3i4PkrIxbDDBNIkQ3F1JFKINYgc5Ty1F1qXelRx1XLSKO5KFYFGjgFDSwHjKtquEiK3haAIpuIWEPFE9ACnzRa3LYKJ6pmIaAl0yWzx8M7osTAzCIE2094GKZlqWzeddujiPLe+JaMtggbL7RsoznYaJ1CmgIViYMe00xeDeJ4U4M43uqM2G9bQxywx5iJqWlhm3CypAZ914VUPrH4IisEq0ED5zKjN2fgrQo0iB5okOZAw9ACjdI6DdNKhq3SgpvmUKOORAM9iQYNSmRpKVS0uU1VAlXocwjQuCrAhVqfq3p5aw4w6q37PChkHDxwVbEFSdmCJGyxtq+KL5Lit7mVTZtpQCVpPIE3yGnzRuvyp13MYRWOv9DK1qaZo3W66JIHLRw+pjvpGuTROp2eKNMRz3h89pbLYFk1sD8qH2a82mepwlX1zG+Do3q3eO8wUf4QNw+VplfevFXLcK0nwHXbTF+1QIS+gK2VmP22Bma/0zHxu9Zgdre4zsZCSr8mL2HsauQmOV54ewbeqZCb6iE3bXxuz6wvSm7yiCrnjhpdTlhHoYGeQoMGFUoWfNKaAhVmX9cxqaDQAR5pqYTuzaeNtsp0pYNxiqG6hRDeaFirAnKaAjnNAfl2LKc5LN+E868Sxe/2Am/6PYB36/CB9AgxuOcZtsWzSROZ1QsIKyYBcXrtYyCI7SJ9bZEwSoDTmFhipTd4Hq0sdy2S5Tuaj62BIe9qYMh7nfH7fcPpVrfm8zUlAkQpAeacALGDMgrNpVbvzsB7FaOYeoxiNj4tWDcFLjxSAy2mfKamWUqpo9FAT6NBgxqZehIpVoNqKHRASFGgilqrK/15p0pgaSO2NBjoqqjFTKnFVFDLdnYxFeySI5jNKcW7J0wjmt8PzbSOaQShQIwtSBijho3tnUyDj3lWZAfTtE6eUq4M9R7SgfbJiHPXOnF+55vNseZ9Db75oDPcf2jPNEv6dkPcoxQxiHmaZRkGNaBcHHRAbDFzadb7M/BBhS1MD1tY49hSd2ql+DIqqn4ZFUVNYksdjQZ6Gg0a1EhvOWO3vHBRqVCDT06pcuDdivX15uH7bZuHP3QMqyISlhIJk6NEv/qhqaToLMcbCup4Anuwk2aPWYuyJSzg2DRtg2GLUWLaW6ZP0nU4+XeIsNN5HcDXluJg/ZmU9XvHCnxyKhLdtVSi72itaQ3q+FCDOq60bjK2hzqKtxOTZLe4OMIkByUQlsuVPpyBKxWBWHoEYh3L0qHSq8hIJkpuzReuyG8PQyB1NBroaTRoUCNL690NpYkTs0Ij0uD6rn7hoSq1Rn39SZL+MUyMHDKSVXGIlXKIlXDI9tmQpPhMMQOyg0ueQCfWadNJ63IrjRVeElHYCb0iTuXN7ZFGm0yKt9uPKfHVIJPWCfXElzyc2KzIVQ0+udYZ36/bwyfFhQ0kUbo42sOD8omVy6uuzsC1ik9sPT6xG58hqbvYrpjkJs82lBd8NckndTQa6Gk0aFIjpAcoxTVcFRLZTfKJYl5ErVN/3+Vc/e0DWJseFz1kZKviFTvlFTvHK9upxc5Ryya7zCWp+Htxif09cEnrMiurZ1mQWQTajAMIomjXWi1oFJ8/OaLkartG8xbpUh9NmApNkHE6j5/4LZKl+t/MqVosd0Qy1ECP6xro8VFnwP7YHvSgPcYwpDZDlkENC5LsLU3dQ79fzs7lSNdn4KOKN/4HGv+rhxzxL5rKaPX+BZ3i6h6arvopLtciTUJHHaEG2kINjkmoouVxhU5mgw+V9Au56i7J+vr32isppI0scvBQVwUgsZ8nDJLsFzFkO4yIWxklGskxyeYciv+EeRN+pe8GUFqHKVteoVi10Ktw/JgSsR2Y0jp1yk+UWHorvE7niRK/deJUI0tCjqS4JPKIxKiBLB9rIMsnndH9U2uQpbjWgTD1LcXD/sOf6zE9ybE+noFPan6B2vwCm0uLLa20uPg+qOQd2crFXs3xS02tBtpaDZrVKp3hqt+R8ivtkFos3PzsSSXJqJW70RHtplWU0mR0q+YVuMErMOGVm0o6SRbkBTkWURDJU7gEnjSXBK1KpepTiHK25Jj+sZFaENK6bLc+iihv2CMDns6aLr+lGu0kkuIyO3JMr7irgSSfaiBJX+uGY2uQpDA4W+lrvQqLHw5NJDCf5X46A301kSBtIkGNE0nNp6iLjzBA5RMMyMDNAkktqQbaUg3aIFX26pSdz7WWFtappKp4I8EhaOSmhkg3+jMnNy2cLWkwpFVjCNrAEJRiyI6pkuRf3w0U0yM7wOQpeIJOG09amF1hjJDJTGRTyn2WWdWQkj5vkjt4cjMlLU2Dt6GK8jGG0xFGFVzaI4zm0ybFpXdHq1J+KP7zfoOwEQtiPH0Adnxv7og2cmu4C2EjEC5cdxzvyQrznQU/HbdJzgQbXYylqGk907KGbRb7jxOw2LMbLJ/Q9IPRKtySzvzj7+UschmFvDN57o5XJc3iU2eJ5PpXtQPLKPDHnrQfL36TlB5uV8zYXy/9EFHticMgmLnOOvsaxs3mV1u5pRChyz/7NXcNP0hmzGz7zJmziE0fH8vUA5/1/WlQ05/QXv6EnupPz2bgg/qT2z5/gsb2Gx9qhxoU280dwA95RePxVHyeusHUHS6dn/4JUEsHCPozDo8AEgAAer4AAFBLAQIUABQACAAIAO91bz/WN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgA73VvP/ozDo8AEgAAer4AAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACXEgAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | =Aufgabe 4.4= | ||
| + | Sowohl die Punkte <math>M_i, 0<i<13, i \in \mathbb{N}</math> als auch die Punkte <math>N_i, 0<i<13, i \in \mathbb{N}</math> sind zueinander Bilder bei Drehungen um das Zentrum <math>Z_M</math> bzw. <math>Z_N</math>. Berechnen Sie die Koordinaten dieser Drehzentren. | ||
[[Kategorie:Elementargeometrie]] | [[Kategorie:Elementargeometrie]] | ||
Aktuelle Version vom 16. November 2011, 12:23 Uhr
Zu den Lösungen Serie 04 WiSe 2011/12
Inhaltsverzeichnis |
Aufgabe 4.1
Es seien  drei nichtkollineare Punkte und
drei nichtkollineare Punkte und 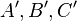 ihre Bilder bei der Bewegung
ihre Bilder bei der Bewegung  . Man beweise: Für jeden Punkt
. Man beweise: Für jeden Punkt  ist jetzt sein Bild
ist jetzt sein Bild 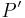 bei
bei  eindeutig bestimmt.
eindeutig bestimmt.
Aufgabe 4.2
Es seien  und
und  zwei Geraden, die sich in genau dem Punkt
zwei Geraden, die sich in genau dem Punkt  schneiden. Man beweise:
Die Nacheinanderausführung
schneiden. Man beweise:
Die Nacheinanderausführung 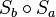 ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden
ist eine Drehung um Z, wobei der Drehwinkel dieser Drehung doppelt so groß ist wie der Winkel zwischen den beiden Geraden  und
und  .
.
Aufgabe 4.3
Sie haben mit Ihren Schülern den Begriff der Drehung erarbeitet. Jetzt steht eine Erstfestigung an. Entwickeln Sie Fragestellungen, die sich auf die folgende Geogebra-Applikation beziehen und der Festigung des Begriffs der Drehung dienen. Beispiele:
- Der Punkt
 wird bei einer Drehung um
wird bei einer Drehung um  auf den Punkt
auf den Punkt  abgebildet. Wie groß ist der Drehwinkel dabei?
abgebildet. Wie groß ist der Drehwinkel dabei?
- Ist es möglich, dass bei einer Drehung um
 der Punkt
der Punkt 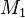 auf den Punkt
auf den Punkt  abgebildet wird?
abgebildet wird?
Aufgabe 4.4
Sowohl die Punkte 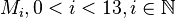 als auch die Punkte
als auch die Punkte 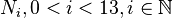 sind zueinander Bilder bei Drehungen um das Zentrum
sind zueinander Bilder bei Drehungen um das Zentrum 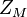 bzw.
bzw. 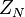 . Berechnen Sie die Koordinaten dieser Drehzentren.
. Berechnen Sie die Koordinaten dieser Drehzentren.

