Die Satzgruppe des Pythagoras: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) (→Satzfindung - Reduktive Methoden (Induktion/Funktionale Betrachtung/(Umkehrung)/(Verallgemeinerung)) |
*m.g.* (Diskussion | Beiträge) (→Beweis von Leonardo da Vinci) |
||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | |||
==Satz des Pythagoras== | ==Satz des Pythagoras== | ||
| Zeile 80: | Zeile 78: | ||
'''Wir werden das in der Vorlesung ausprobieren.''' | '''Wir werden das in der Vorlesung ausprobieren.''' | ||
| + | |||
| + | ===Umkehrung=== | ||
| + | Die Umkehrung des Satzes lässt sich vor allem enaktiv wunderbar herstellen. Man gebe den Schülern verschiedenfarbige (bestenfalls auch noch mit dem Flächeninhalt beschriebene) Quadrate und diese sollen sie so legen, dass ein Dreieck herauskommt. Was haben wohl die Quadrate gemeinsam, für die die Summe der Flächeninhalte zweier Quadrate gleich dem Inhalt des dritten Quadrates ist?<br /><br /> | ||
| + | |||
| + | '''Wir werden das in der Vorlesung ''nicht'' ausprobieren.'''<br /> | ||
| + | Wir werden diesen Aspekt aber in der Arbeitsphase am Satz nochmal aufgreifen - dann ist es genauso interessant und wichtig. | ||
| + | |||
| + | ===Analogieüberlegung=== | ||
| + | Die Analogie macht hier wahrscheinlich nicht allzuviel Sinn, obgleich es eine Möglichkeit der Satzfindung darstellt. Wenn man die Möndchen des Hyppokrates ([http://de.wikipedia.org/wiki/M%C3%B6ndchen_des_Hippokrates]) nutzen möchte, so ist dies wahrscheinlich eher geeignet, um über den klassischen Tellerrand hinauszuschauen und Aspekte wie Argumentieren und ähnliche mathematische Kompetenzen zu festigen. | ||
| + | |||
| + | '''Wir werden die Möndchen nicht in der Vorlesung betrachten.''' | ||
<ggb_applet width="1350" height="591" version="4.0" ggbBase64="UEsDBBQACAAIALS5dD8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAC0uXQ/AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c25Lbthm+dp4Co4tedCwuARA8pFpnZDtONlnHmdjtdHrjoUhIopciFZLalTJ5qLSPkAfoM/UHQEqkJEqi1jqtu+M1SJzxf/8RALfzzXQUonuepEEcXbewprcQj7zYD6LBdWuS9dt265sXX3UGPB7wXuKifpyM3Oy6ZYiagQ9NPMtnPcdp647jtQ3q8rZN/F7bwRybhHg+Jf0WQtM0+DqKf3JHPB27Hn/vDfnIvY09N5MDD7Ns/PXV1cPDg1YMpcXJ4Gow6GnT1G8hmGaUXrfyh6+hu0qjByqrE13HV/98e6u6bwdRmrmRx1tILGESvPjqWechiPz4AT0EfjaE2VPTbKEhDwZDWJRF7Ba6ErXGQJEx97LgnqfQtvQqF52Nxi1ZzY1E+TP1hML5elrID+4DnyfXLV2jzDEMalKsU4dRzFooTgIeZXldnI95VfTWuQ/4g+pWPMkRjRbK4jjsuaJH9PvviOhER89FglVCIDFNVaSrPJ2qhKjEUAlTdQzV3FBVDVXHUHUM2kL3QRr0Qn7d6rthCiQMon4C8M3f02wWcjmfPGOxevwc1pQGv0FlqgOfKJpDvq4/F78m/Bqi4Kq6SFwaNUsmDQcthsSUNRiTPGqltBjUcPDqmITVrNPcMKha+E4LLa8ThpL/5O/KiHTTMpdHVO+PG9A0jrLEzlUhK51cPFA6FHVz9sn4KBUCQx3EHMH3GDEQDtMCNmcIO5BYBIE4IMyQweAV28gUqYWoBQUGoshGoh6mSEoHs+E/w5KdmYhBZyLXAqFEGAYyEKMIS6EyEIgSkoIJQkoo1GAMMWgkhsdEdEFNZJjwRm1kwByFTFoYKlJoCO8wPEEUIyoaYwsRE5miP2wIWTdtMXXokiBTRyYWHYJYg0grcYb6NqJiNWZOriAaT7IKibyRXzxm8XiOBdQGhbRQe0pBVbTis07o9ngIluK9QBKhezcUEiEH6sdRhgoQicobJO54GHjpe55l0CpFn9x799bN+PQN1E6LsWVdL47Sn5M4exWHk1GUIuTFoT6fcxzi0jOZzxpeaKnAKBewUoFZerbWjhtDCZqkHMaPk7So7vr+jaixUA1AyXdROHuZcPduHAfVZXSupNHp8IkXBn7gRv8AZhWjCLqghQ0STF7YIGbSYiZx4r+fpcDCaPovnsRCiqlmM4eB0qaEUKArmqkSYlGNmDqlOrNshgm1YG6eK4TPIGCAGLWwo+s2MQ0QzFlNka1G5vdzhNwpXyx2kAjJLr3cpC/jcJEl1//KHWeTRLoPoBwTsahuNAi55BGpbsE2e3e9ePo+19aqrw+zMbzpaga9gaQ7At1AGNjLQZ72VCrriKnNa+myji5r6AW3Bf68HDtE1pBpT6WyFrCvmlq+VFwsE+vFMEEqNZreyuWm0FaC+YWln0RBdlu8ZIF3ly8VqwY/TUY9Pmehap/4c/XZuVrisc4dTyIe5iwNYE7iSaoktMTtPveCEbyqgpwkroDr7zABlevzQcKLiYfSNVMEk6V6mVlXsmVXb5J4dBPdfwBeWJpA56qYZSf1kmAseA71wAzc8QVX+UHqghXxy+2EDMLSPWEtgDyZIA1I5yQbxol0vkCpQCprjkZu5KNIGp6fBYe2ForQBZUy7QIaarrxJCtyu2p+eXMhwyEfgc+GMsmnktXneHVllwIYFPc+gYKc21BVvkAeihc8SRRnyzTnbOSG46ErnMacgqE740mFprLPd/1+yjM0vW61hajPoLVZKn4b+8tAAM6SWqBPxoqPxpwrFlRLgocxjCYlt6IQAdlUjCRd/pmaG/pNBQvKWRbEENJcsQAqd4klgE8VHR8Bzcsm0Lw8ITS2JBdmhwbG0QzzgMi85wORv4RNFwiCczAq8LgfyWaA0ry/AgLRYAWkqkIsLbsMU1Xr7wrQCgYLSuo5izOgqF76wZKsi47nRiMDf+YOorZUWrYst2Hy4fvA97n0ZZVR/TVSTVKlyYPROAy8IJvTLxQI30QZ6HUuFduqur7jfCzs5LvoQ+JGqYjFVZ2SGagB8W3gj9dIWA5WBcBXH3ETCRPVt8C3XshEiDBQSU8ljwfQ1Cx6QFF4FSReyJdoKAhQIwveNlKCIQu8OZ287aQ8rCTsxdjBgEf3MFXwkxGa6vku0kwvQChypkCitpIwnGf9hksIgR5MginqFvW7Ra0uOPjU0mzgkC7Ne+2Cb99WaHdZ3u9aORMBS9AHIje2Pjl4VdloJBmndAscKQaQNDA+uraP+ZnLHIGHstbUjQOI4LsEnLxBHLnhLTDrsigqQVyn1fhm5ATnz4Hh52KP2msMUUm5USC9wexS6UHMUz0Yc3O1hAOvx+F1Ewl6fWTLUpIfRWmCdwOK6LpmUqKbdhmndgEUcTQbY3MZqM/kOIczkIc69wy5JFdbFRggSgwhDM8tl6equZCAgu1tg0gNWGAw72pf3qvXkDVyhhmVADO8Imq4iaiVibrZR/X2U+X189yVD3NG2hzdPU0HdkvUcCpE2kRvpBra68zirCZf6Aqm2aSk1HX7yWDWO5kUWc20eTPE2ljXHFLOX9lcPGPIqtbklzhzs2W36qWyEsTS//rnH8pUdFe3Zf7ijuP0b402Z/Im+3lbj3GUN4BPNaf6o7Bfr1GP6Nt2C1O9THi/gWfrX4hnSzCEe+ViemzXdiMWBeNKRPwVRPoNEOmfDSKF71DD6u0aJ/Zsoo3+aqzRbCfr9d7bL4fYyqoJKbAJVsjClBZA2CeKMCoy8FrugRERsckQYtU85FECUfV788bQxpeNoRWXD4YIHLcCtzYGIZ8nBtkJc+GOlM4lxeuho5Deo+zlpgk/esd82TUiyjwamqMffoPiBK6sv7euOAgM57FRdAIc+JnhMDeiywIh7jk8tRD8vGi/XgTatmbb2LIN7FiQRxj5ti3u30mP5khe5hHitvWHtPl++OsVazzcbF6XkR7utw+7n49aCttV7LXxDGNr1L4Bf2xr1CLOogXbBX9yQQzQrWOAcTMGGO/HAEd1OXIN274sFbsLii/rUPy1GYq/nkaMi7OUHeW4bEJJZSeGXT7A8i5kHbw1ZzX//fdmmOUtuzmGUFu0h/lMcgpjjVm65UAwaVqOYTvWviFPcRcz34ndK+R5xNaom3iLUJYUZ9hhGD/8wvshn0ra7grExmOzVwoKoy6KpcX5JlUVvY9ERbDDIoINIGHXrW8hMa9bb/aKZukhotmNijoHtrqTuiuyxb1ldyyvFMi83p//aepT0sf5lGuXsL8/X+NU1F11uOSDgC0noHvf0jsqMF/gqdrwsWHY50WGFNeB6qCgmmOXkTCsJwNFcG5AVPzjTZpr9QzzkmLhTbv63576dqo7mQZh4Caz6vzXXa0/zCHjJuq8uQDqYI2YlTjAXB//HeBEdtfj8NXQLD8eaXYCtWi0FyoHOhE3yxp9XUR2xFPwBYUkBnyF7oPN9K6cvQ4u5uw1P0g5jEpufuI6qDv5/q4Jt393at1TUjHY0YhhLjaDc2/Sxhq1mVmcweZwnOw657a41CjiUqOIS6mKSz+pqPRORaXfq6j0Zq+o1DjAPc/mu4eNthuahJ/GljtqRz1N+n/0OY8+12wLnB0uX2Dw+emMYPmSI8+7M8NhyYf5EgPP70/t3px14HlzAdQ5YeC53g18Vfmqp9YNZPlV4cIN7BUX7ELlBo6UG/iDcgN/3MsNZEdzAz/bqVMTd2NPN3DTXD+bPt3sBbafsLfRW7czcjJc2mTLl685Ek+G/OG5EX/Vy6hz/Qwd8sshu/FkUBmdESpf1JdTm9ybHy7BvSEadsrEXzjqB3f/frwA+sz/rs4xvv2q+chCeXLdLQ6fmX9VIa+hiA+5PzLl8EXK4UuUw3erHL63ezl85tEcvvL2+n5XURq6e711dxt20aH1M3307caak4DLuvu2bbOVnQ3ZgdpszVefhmYYug0myrGZrpvErF4ep9Xg8KkAE50NLFizLJMyEyhtgHPAdAYAsA1KWR3NlKDc6Ur3RaCSnA0qW742YlgzWdnXvlzJqDottxfgtKx8vm7Ozcmygjuwi/f2Aqg1d/EO9H3/VfkvlYr34q/bv/gfUEsHCFvqKLftCwAAel8AAFBLAQIUABQACAAIALS5dD9FzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAtLl0P1vqKLftCwAAel8AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACFDAAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="1350" height="591" version="4.0" ggbBase64="UEsDBBQACAAIALS5dD8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAC0uXQ/AAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1c25Lbthm+dp4Co4tedCwuARA8pFpnZDtONlnHmdjtdHrjoUhIopciFZLalTJ5qLSPkAfoM/UHQEqkJEqi1jqtu+M1SJzxf/8RALfzzXQUonuepEEcXbewprcQj7zYD6LBdWuS9dt265sXX3UGPB7wXuKifpyM3Oy6ZYiagQ9NPMtnPcdp647jtQ3q8rZN/F7bwRybhHg+Jf0WQtM0+DqKf3JHPB27Hn/vDfnIvY09N5MDD7Ns/PXV1cPDg1YMpcXJ4Gow6GnT1G8hmGaUXrfyh6+hu0qjByqrE13HV/98e6u6bwdRmrmRx1tILGESvPjqWechiPz4AT0EfjaE2VPTbKEhDwZDWJRF7Ba6ErXGQJEx97LgnqfQtvQqF52Nxi1ZzY1E+TP1hML5elrID+4DnyfXLV2jzDEMalKsU4dRzFooTgIeZXldnI95VfTWuQ/4g+pWPMkRjRbK4jjsuaJH9PvviOhER89FglVCIDFNVaSrPJ2qhKjEUAlTdQzV3FBVDVXHUHUM2kL3QRr0Qn7d6rthCiQMon4C8M3f02wWcjmfPGOxevwc1pQGv0FlqgOfKJpDvq4/F78m/Bqi4Kq6SFwaNUsmDQcthsSUNRiTPGqltBjUcPDqmITVrNPcMKha+E4LLa8ThpL/5O/KiHTTMpdHVO+PG9A0jrLEzlUhK51cPFA6FHVz9sn4KBUCQx3EHMH3GDEQDtMCNmcIO5BYBIE4IMyQweAV28gUqYWoBQUGoshGoh6mSEoHs+E/w5KdmYhBZyLXAqFEGAYyEKMIS6EyEIgSkoIJQkoo1GAMMWgkhsdEdEFNZJjwRm1kwByFTFoYKlJoCO8wPEEUIyoaYwsRE5miP2wIWTdtMXXokiBTRyYWHYJYg0grcYb6NqJiNWZOriAaT7IKibyRXzxm8XiOBdQGhbRQe0pBVbTis07o9ngIluK9QBKhezcUEiEH6sdRhgoQicobJO54GHjpe55l0CpFn9x799bN+PQN1E6LsWVdL47Sn5M4exWHk1GUIuTFoT6fcxzi0jOZzxpeaKnAKBewUoFZerbWjhtDCZqkHMaPk7So7vr+jaixUA1AyXdROHuZcPduHAfVZXSupNHp8IkXBn7gRv8AZhWjCLqghQ0STF7YIGbSYiZx4r+fpcDCaPovnsRCiqlmM4eB0qaEUKArmqkSYlGNmDqlOrNshgm1YG6eK4TPIGCAGLWwo+s2MQ0QzFlNka1G5vdzhNwpXyx2kAjJLr3cpC/jcJEl1//KHWeTRLoPoBwTsahuNAi55BGpbsE2e3e9ePo+19aqrw+zMbzpaga9gaQ7At1AGNjLQZ72VCrriKnNa+myji5r6AW3Bf68HDtE1pBpT6WyFrCvmlq+VFwsE+vFMEEqNZreyuWm0FaC+YWln0RBdlu8ZIF3ly8VqwY/TUY9Pmehap/4c/XZuVrisc4dTyIe5iwNYE7iSaoktMTtPveCEbyqgpwkroDr7zABlevzQcKLiYfSNVMEk6V6mVlXsmVXb5J4dBPdfwBeWJpA56qYZSf1kmAseA71wAzc8QVX+UHqghXxy+2EDMLSPWEtgDyZIA1I5yQbxol0vkCpQCprjkZu5KNIGp6fBYe2ForQBZUy7QIaarrxJCtyu2p+eXMhwyEfgc+GMsmnktXneHVllwIYFPc+gYKc21BVvkAeihc8SRRnyzTnbOSG46ErnMacgqE740mFprLPd/1+yjM0vW61hajPoLVZKn4b+8tAAM6SWqBPxoqPxpwrFlRLgocxjCYlt6IQAdlUjCRd/pmaG/pNBQvKWRbEENJcsQAqd4klgE8VHR8Bzcsm0Lw8ITS2JBdmhwbG0QzzgMi85wORv4RNFwiCczAq8LgfyWaA0ry/AgLRYAWkqkIsLbsMU1Xr7wrQCgYLSuo5izOgqF76wZKsi47nRiMDf+YOorZUWrYst2Hy4fvA97n0ZZVR/TVSTVKlyYPROAy8IJvTLxQI30QZ6HUuFduqur7jfCzs5LvoQ+JGqYjFVZ2SGagB8W3gj9dIWA5WBcBXH3ETCRPVt8C3XshEiDBQSU8ljwfQ1Cx6QFF4FSReyJdoKAhQIwveNlKCIQu8OZ287aQ8rCTsxdjBgEf3MFXwkxGa6vku0kwvQChypkCitpIwnGf9hksIgR5MginqFvW7Ra0uOPjU0mzgkC7Ne+2Cb99WaHdZ3u9aORMBS9AHIje2Pjl4VdloJBmndAscKQaQNDA+uraP+ZnLHIGHstbUjQOI4LsEnLxBHLnhLTDrsigqQVyn1fhm5ATnz4Hh52KP2msMUUm5USC9wexS6UHMUz0Yc3O1hAOvx+F1Ewl6fWTLUpIfRWmCdwOK6LpmUqKbdhmndgEUcTQbY3MZqM/kOIczkIc69wy5JFdbFRggSgwhDM8tl6equZCAgu1tg0gNWGAw72pf3qvXkDVyhhmVADO8Imq4iaiVibrZR/X2U+X189yVD3NG2hzdPU0HdkvUcCpE2kRvpBra68zirCZf6Aqm2aSk1HX7yWDWO5kUWc20eTPE2ljXHFLOX9lcPGPIqtbklzhzs2W36qWyEsTS//rnH8pUdFe3Zf7ijuP0b402Z/Im+3lbj3GUN4BPNaf6o7Bfr1GP6Nt2C1O9THi/gWfrX4hnSzCEe+ViemzXdiMWBeNKRPwVRPoNEOmfDSKF71DD6u0aJ/Zsoo3+aqzRbCfr9d7bL4fYyqoJKbAJVsjClBZA2CeKMCoy8FrugRERsckQYtU85FECUfV788bQxpeNoRWXD4YIHLcCtzYGIZ8nBtkJc+GOlM4lxeuho5Deo+zlpgk/esd82TUiyjwamqMffoPiBK6sv7euOAgM57FRdAIc+JnhMDeiywIh7jk8tRD8vGi/XgTatmbb2LIN7FiQRxj5ti3u30mP5khe5hHitvWHtPl++OsVazzcbF6XkR7utw+7n49aCttV7LXxDGNr1L4Bf2xr1CLOogXbBX9yQQzQrWOAcTMGGO/HAEd1OXIN274sFbsLii/rUPy1GYq/nkaMi7OUHeW4bEJJZSeGXT7A8i5kHbw1ZzX//fdmmOUtuzmGUFu0h/lMcgpjjVm65UAwaVqOYTvWviFPcRcz34ndK+R5xNaom3iLUJYUZ9hhGD/8wvshn0ra7grExmOzVwoKoy6KpcX5JlUVvY9ERbDDIoINIGHXrW8hMa9bb/aKZukhotmNijoHtrqTuiuyxb1ldyyvFMi83p//aepT0sf5lGuXsL8/X+NU1F11uOSDgC0noHvf0jsqMF/gqdrwsWHY50WGFNeB6qCgmmOXkTCsJwNFcG5AVPzjTZpr9QzzkmLhTbv63576dqo7mQZh4Caz6vzXXa0/zCHjJuq8uQDqYI2YlTjAXB//HeBEdtfj8NXQLD8eaXYCtWi0FyoHOhE3yxp9XUR2xFPwBYUkBnyF7oPN9K6cvQ4u5uw1P0g5jEpufuI6qDv5/q4Jt393at1TUjHY0YhhLjaDc2/Sxhq1mVmcweZwnOw657a41CjiUqOIS6mKSz+pqPRORaXfq6j0Zq+o1DjAPc/mu4eNthuahJ/GljtqRz1N+n/0OY8+12wLnB0uX2Dw+emMYPmSI8+7M8NhyYf5EgPP70/t3px14HlzAdQ5YeC53g18Vfmqp9YNZPlV4cIN7BUX7ELlBo6UG/iDcgN/3MsNZEdzAz/bqVMTd2NPN3DTXD+bPt3sBbafsLfRW7czcjJc2mTLl685Ek+G/OG5EX/Vy6hz/Qwd8sshu/FkUBmdESpf1JdTm9ybHy7BvSEadsrEXzjqB3f/frwA+sz/rs4xvv2q+chCeXLdLQ6fmX9VIa+hiA+5PzLl8EXK4UuUw3erHL63ezl85tEcvvL2+n5XURq6e711dxt20aH1M3307caak4DLuvu2bbOVnQ3ZgdpszVefhmYYug0myrGZrpvErF4ep9Xg8KkAE50NLFizLJMyEyhtgHPAdAYAsA1KWR3NlKDc6Ur3RaCSnA0qW742YlgzWdnXvlzJqDottxfgtKx8vm7Ozcmygjuwi/f2Aqg1d/EO9H3/VfkvlYr34q/bv/gfUEsHCFvqKLftCwAAel8AAFBLAQIUABQACAAIALS5dD9FzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAtLl0P1vqKLftCwAAel8AAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACFDAAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| Zeile 104: | Zeile 113: | ||
Für die Fußballfans unter euch bedeutet das folgendes: Nur weil man sich für die Champions-League qualifiziert hat '''und''' nur weil das Finale auch noch rein zufällig in München stattfindet, heißt das noch lange nicht, dass man auch die Champions-League gewinnt. | Für die Fußballfans unter euch bedeutet das folgendes: Nur weil man sich für die Champions-League qualifiziert hat '''und''' nur weil das Finale auch noch rein zufällig in München stattfindet, heißt das noch lange nicht, dass man auch die Champions-League gewinnt. | ||
--[[Benutzer:HecklF|Flo60]] 23:26, 20. Nov. 2011 (CET) | --[[Benutzer:HecklF|Flo60]] 23:26, 20. Nov. 2011 (CET) | ||
| + | ===Beweis des Euklid=== | ||
| + | http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/geometrie/pyth/beweise/euklid | ||
| + | ===Beweis von Leonardo da Vinci=== | ||
| + | http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/geometrie/pyth/beweise/vinci | ||
| + | ===Beweis mit Scherungen=== | ||
| + | http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/geometrie/pyth/beweise/scherung | ||
[[Kategorie: Elementargeometrie]] | [[Kategorie: Elementargeometrie]] | ||
Aktuelle Version vom 21. November 2011, 22:31 Uhr
Inhaltsverzeichnis |
Satz des Pythagoras
Satz
Im rechtwinkligen Dreieck ist die Summe der Flächeninhalte der beiden Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrates. 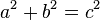
Der Kathetensatz des Euklid
Satz
Im rechtwinkligen Dreieck ist das Quadrat über einer Kathete flächeninhaltsgleich mit dem Rechteck aus der Hypotenuse und dem zur Kathete gehörenden Hypotenusenabschnitt. 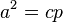 bzw.
bzw. 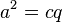
Skizze
Und eine vielleicht etwas ungewohnte Darstellung:
--Flo60 21:50, 19. Nov. 2011 (CET)
Der Höhensatz
Satz
Im rechtwinkligen Dreieck ist das Quadrat über der Höhe aufder Hypotenuse flächeninhaltsgleich mit dem Rechteck aus den Hypotenusenabschnitten. 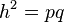
--Flo60 22:13, 19. Nov. 2011 (CET)
Satzfindung - Ein Einstieg
Neulich in Hinterhugelhapfing:
Unser Lehrer (nein, es war nicht Frau oder Herr Schultz-Kröttendorfer) möchte mit seinen Schülern den Satz des Pytagoras einführen. Leider hat unser Lehrer kein allzugroßes Geschichtsbewusstsein und Schule macht ihm auch schon seit 30 Jahren keinen Spaß mehr. Seiner Meinung nach sind die Menschen im Laufe der Geschichte immer schlauer geworden. Ansonsten wären ja schon die Steinzeitmenschen mit Autos gefahren. Seiner Logik folgend gestaltet er auch seinen Unterricht. Den Satz des Pythagoras kannten schon die alten Ägypter. Ja, wenn das so ist, denkt sich der Lehrer, müssen ihn meine Schüler heute ja mit Leichtigkeit verstehen. Drei Minuten und dann können wir Arbeitsblätter machen.
Unser Lehrer startet den Unterricht:
Guten Morgen. Ihr kennt ja schon die rechtwinkligen Dreiecke. Nach dem Satz des Pythagoras kann man nun die Seitenlängen berechnen, wenn man zwei Seiten hat. Man rechnet einfach a² + b² = c². Wir probieren das anahand der Übungsblätter aus.
Was läuft hier falsch?
Man könnte jetzt sagen, naja kein Einstieg, die Erläuterung ziemlich schnell und aber die Arbeitsphase ist da. Wer jetzt denkt, dass das Blödsinn ist, erinnere sich kurz in seine eigene Schulzeit zurück. Vielleicht hat sich die Lehrperson (ob Mann oder Frau ist völlig Banane) dort etwas mehr Zeit gelassen, aber schlussendlich glaube ich haben die Satzfindung viele so erlebt.
Wie könnte man anders vorgehen?
Satzfindung - Reduktive Methoden (Induktion/Funktionale Betrachtung/(Umkehrung)/(Verallgemeinerung)
Was bedeutet Satzfindung?
Im Gegensatz zu jeglicher deduktiven 'Herleitung' von Sätzen können mit reduktiven Methoden Sätze wirklich 'gefungen' werden. Unser Lehrer aus dem Eingangsbeispiel ist stark deduktiv vorgegangen und hat den Satz - mit Verlaub - lediglich hingerotzt. Was der Satz bedeutet und wie er zustande kommt, weiß der Schüler in diesem Falle nicht. Bereits in diesem Teilbereich kann aber der Schüler schon viel lernen. Wenn nämlich der Satz in seiner Bedeutung verstanden ist, dann kann man ihn auch herleiten, ohne die Formel explizit zu wissen. Dies gilt im übrigen für viele andere Sätze auch. Reduktive Methoden lassen den Schüler auf verschiedenste Arten und Weisen Sätze finden bzw. erforschen. Hier bietet sich natürlich auch ein Differenzierungspotential. Allerdings sei angemerkt, dass sich natürlich nicht jede Methode der Satzfindung für jeden Satz eignet. Bereits am Anfang sei kurz angemerkt, dass die Satzfindung alleine noch keine Meister macht - oder um in der Fußballersprache zu sprechen: Nur weil man sich für die Champions-League qualifiziert hat hat man sie noch nicht gewonnen. Es folgen noch zwei weitere Schritte, nämlich die Arbeit am Satz und dann der evtl. Beweis. Zu beiden Teilbereichen später mehr.
Was bedeutet Induktion im Sinne der Satzfindung?
Induktion bedeutet in diesem Zusammenhang (wie in allen anderen Zusammenhängen; vgl. vollständige Induktion der Arithmetik) das Schließen von (einem) Einzelfall auf die Allgemeinheit.
Möglichkeiten:
- Arbeitsblatt mit (am besten) rechtwinkligen Dreiecken (Gegenbeispiele kommen besser erst in der Arbeitsphase)
- Geogebraapplikation
- Papier zum Ausschneiden
- weitere eigene Beispiele
Beim Satz des Pytagoras kommt es schlussendlich darauf an, dass die Schüler eine Messreihe zustandebringen und dadurch auf die Bedeutung des Satzes schließen. Diese kann folgendermaßen Aussehen:
| Beispieldreieck (Nr.) | Fläche (Seitenlänge a)² | Fläche (Seitenlänge b)² | Fläche (Seitenlänge c)² |
| ___ | ___ | ___ | |
| ___ | ___ | ___ | |
| ___ | ___ | ___ | |
| Was fällt dir auf? |
Wir werden das in der Vorlesung ausprobieren.
Funktionale Betrachtung
Desto mehr Satzfindungsmöglichkeiten ich habe, desto größer ist wie beschrieben das Differenzierungspotential - ergo, ich sollte alle Möglichkeiten ausschöpfen, der Schüler dankts ;-).
Die Wahrscheinlich eleganteste Möglichkeit, den Satz des Pythagoras zu finden, bietet aber wahrscheinlich die funktionale Betrachtung. Diese ist nicht ganz trivial zu beschreiben, zu verstehen aber allemal. Entscheident ist, dass eine Größe in Abhängikeit einer anderen Größe verändert wird. Durch die Veränderung der abhängigen Größe können nun Schlüsse auf den Satz gezogen werden.
Wir werden das in der Vorlesung ausprobieren.
Umkehrung
Die Umkehrung des Satzes lässt sich vor allem enaktiv wunderbar herstellen. Man gebe den Schülern verschiedenfarbige (bestenfalls auch noch mit dem Flächeninhalt beschriebene) Quadrate und diese sollen sie so legen, dass ein Dreieck herauskommt. Was haben wohl die Quadrate gemeinsam, für die die Summe der Flächeninhalte zweier Quadrate gleich dem Inhalt des dritten Quadrates ist?
Wir werden das in der Vorlesung nicht ausprobieren.
Wir werden diesen Aspekt aber in der Arbeitsphase am Satz nochmal aufgreifen - dann ist es genauso interessant und wichtig.
Analogieüberlegung
Die Analogie macht hier wahrscheinlich nicht allzuviel Sinn, obgleich es eine Möglichkeit der Satzfindung darstellt. Wenn man die Möndchen des Hyppokrates ([1]) nutzen möchte, so ist dies wahrscheinlich eher geeignet, um über den klassischen Tellerrand hinauszuschauen und Aspekte wie Argumentieren und ähnliche mathematische Kompetenzen zu festigen.
Wir werden die Möndchen nicht in der Vorlesung betrachten.
--Flo60 23:15, 20. Nov. 2011 (CET)
Festigung des Satzes durch Arbeit am Satz
Was ist Arbeit am Satz
Nachdem die Schüler den Satz gefunden haben, kann es entweder sein, dass die Stunde vorbei ist oder man noch Zeit hat um weiter zu arbeiten. In beiden Fällen muss der Satz aber gefestigt werden. Dies beinhaltet verschiedene Aspekte die den Satz selbst betreffen und Aspekte, die den Satz nur indirekt betreffen (z. B. was ist die Hypotenuse). Schlussendlich kommt es durch gezielte Aufgaben darauf an, dass auch jeder (soweit das natürlich möglich ist - aber das sollte der Anspruch sein) den Satz verstanden hat. Finden heißt nicht gleichzeitig verstehen und oftmals gar nicht beherrschen.
Wieso braucht man Arbeit am Satz?
Naja, nur weil der Satz gefunden ist, heißt das noch nicht, dass ihn auch erstens
- jeder verstanden hat und zweitens
- jeder anwenden kann und drittens besteht die Möglichkeit,
- dass einzelne Teilaspekte nicht klar sind.
Wir werden im Folgenden verschiedene Aspekte aufgreifen, die speziell für den Satz des Pythagoras von Relevanz sind. Der Sinn des Ganzen sollte aber dadurch klar werden und Analogien können sicherlich zu anderen Sätzen gezogen werden.
Beweise der Satzgruppe des Pythagoras
Es ist kurz von Bedeutung, folgendes vorwegzuschicken:
Inwieweit man mit den Schülern den Satz des Pythagoras oder eine Abwandlung dessen überhaupt beweist, hängt von der Klassenstärke ab bzw. vom Verständnis des Einzelnen. Vielleicht lässt man auch nur den einen oder andere Schüler beweisen. Wichtig ist aber, dass die Arbeit am Satz vollzogen wurde und jeder den entsprechenden Satz verstanden hat. Die Arbeit am Satz ist wichtiger als der Beweis selbst. Der beste Beweis hilft mir nichts, wenn ich nicht verstanden habe, um was es eigentlich geht.
Für die Fußballfans unter euch bedeutet das folgendes: Nur weil man sich für die Champions-League qualifiziert hat und nur weil das Finale auch noch rein zufällig in München stattfindet, heißt das noch lange nicht, dass man auch die Champions-League gewinnt.
--Flo60 23:26, 20. Nov. 2011 (CET)
Beweis des Euklid
http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/geometrie/pyth/beweise/euklid
Beweis von Leonardo da Vinci
http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/geometrie/pyth/beweise/vinci
Beweis mit Scherungen
http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek1/geometrie/pyth/beweise/scherung

