Übung vom 18.11.11: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Definition 3) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 4) |
||
| Zeile 25: | Zeile 25: | ||
Selbst wenn man Scheitelwinkel irgendwie ausschließen könnte wären nur rechte Winkel als Nebenwinkel zugelassen. --[[Benutzer:*m.g.*|*m.g.*]] 14:50, 22. Nov. 2011 (CET)<br /> | Selbst wenn man Scheitelwinkel irgendwie ausschließen könnte wären nur rechte Winkel als Nebenwinkel zugelassen. --[[Benutzer:*m.g.*|*m.g.*]] 14:50, 22. Nov. 2011 (CET)<br /> | ||
| − | =Aufgabe 4= | + | =Aufgabe 4: Definition Scheitelwinkel= |
| − | + | ==Definition 1== | |
[[Datei:Aufgabe 4.jpg|400px]]<br /> | [[Datei:Aufgabe 4.jpg|400px]]<br /> | ||
| − | + | ==Definition 2== | |
[[Datei:Aufgabe 4-and.Loesung.jpg|400px]]<br /><br /> | [[Datei:Aufgabe 4-and.Loesung.jpg|400px]]<br /><br /> | ||
alternative Lösung (intuitiv)<br /> | alternative Lösung (intuitiv)<br /> | ||
Version vom 22. November 2011, 14:52 Uhr
Hier findet ihr alle Aufgaben und Lösungen/Lösungsversuche:
Inhaltsverzeichnis |
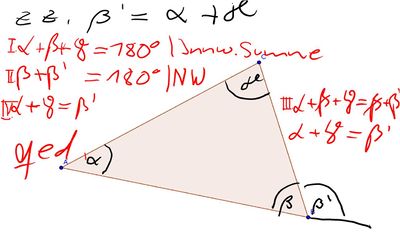
Aufgabe1: Starker Außenwinkelsatz für Dreiecke
Aufgabe 2: Beispiele/Gegenbeispiele für Nebenwinkel
Aufgabe 3: Definition Nebenwinkel
Definition 1
Definition 2

Lösung nur bedingt richtig, da zu ungenau (was ist nebeneinander liegen?)
Definition 3

Lösung zu ungenau, da auch die Scheitelwinkel in Frage kommen könnten.
Selbst wenn man Scheitelwinkel irgendwie ausschließen könnte wären nur rechte Winkel als Nebenwinkel zugelassen. --*m.g.* 14:50, 22. Nov. 2011 (CET)
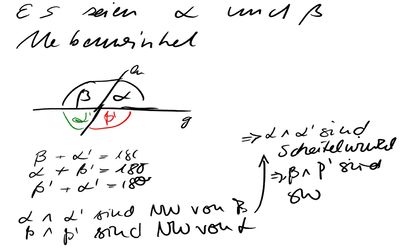
Aufgabe 4: Definition Scheitelwinkel
Definition 1
Definition 2

alternative Lösung (intuitiv)

mögliche daraus resultierende Lösung

Aufgabe 5
Definieren Sie den Begriff Scheitelwinkel unter Verwendung des bereits definierten Begriffs Nebenwinkel
Aufgabe 6

selbst falls A auf SA+ liegt, ist diese Lösung richtig, da sich daraus ein Nullwinkel bzw ein 360°-Winkel ergibt.

hier wird nicht der Winkel sondern das Innere eines Winkels definiert.
--Adores 23:17, 21. Nov. 2011 (CET)