Übung vom 25.11.11: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Adores (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 6: Beweis Zwischenrelation: \operatorname{Zw} (A, B, C) \Rightarrow \neg \operatorname(Zw) (B, A, C)) |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
=Aufgabe 2: Addition zweier Strecken (<math>\overline{AB}</math> + <math>\overline{BC}</math> =) = | =Aufgabe 2: Addition zweier Strecken (<math>\overline{AB}</math> + <math>\overline{BC}</math> =) = | ||
| − | |||
[[Datei:2Aufgabe 2.jpg|400px]]<br /> | [[Datei:2Aufgabe 2.jpg|400px]]<br /> | ||
<br /> | <br /> | ||
| Zeile 23: | Zeile 22: | ||
[[Datei:2Aufgabe 3.jpg|400px]]<br /> | [[Datei:2Aufgabe 3.jpg|400px]]<br /> | ||
<br /> | <br /> | ||
| − | --> Lösung nur bedingt richtig, je 3 von 4 Punkten müssten kollinear sein (siehe Schaubild)<br /> | + | --> Lösung nur bedingt richtig, je 3 von 4 Punkten müssten nicht kollinear sein (siehe Schaubild)<br /> |
<br /> | <br /> | ||
==Definition 2== | ==Definition 2== | ||
| Zeile 32: | Zeile 31: | ||
<br /> | <br /> | ||
| − | =Aufgabe 4: Definition | + | =Aufgabe 4: Definition Viereck (mit Hilfe von Dreiecken)= |
==Definition 1== | ==Definition 1== | ||
| − | [[Datei: | + | [[Datei:2Aufgabe 4.jpg|400px]]<br /> |
| − | + | <br /> | |
| + | --> hier ist zu beachten, dass man B und C wieder aufführen muss, da sie aufgrund der Entfernung der Strecke <math>\overline{BC}</math> wegfallen.<br /> | ||
| + | <br /> | ||
==Definition 2== | ==Definition 2== | ||
| − | [[Datei: | + | [[Datei:2Aufgabe 4.1.jpg|400px]]<br /> |
| − | + | <br /> | |
| + | --> die oben genannte Problematik entfällt, wenn man die offene Strecke <math>\overline{BC}</math> verwendet, da in dieser die Punkte B und C nicht enthalten sind. <br /> | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
| − | + | ||
| − | =Aufgabe 5: | + | =Aufgabe 5: Definition Außenwinkel eines Dreiecks= |
== Definition 1== | == Definition 1== | ||
| − | + | [[Datei:2Aufgabe 5.jpg|400px]]<br /> | |
| − | + | <br /> | |
| − | [[Datei: | + | -->intuitive Definition, da anliegen kein mathematisch korrekter Ausdruck ist.<br /> |
| + | <br /> | ||
==Definition 2== | ==Definition 2== | ||
| − | [[Datei: | + | [[Datei:2Aufgabe 5.1.jpg|400px]]<br /> |
| − | + | <br /> | |
| − | + | ||
<br /> | <br /> | ||
| − | =Aufgabe 6: | + | =Aufgabe 6: Beweis Zwischenrelation: <math>\operatorname{Zw} (A, B, C) \Rightarrow \neg \operatorname{Zw} (B, A, C) </math> = |
| − | + | [[Datei:2Aufgabe 6.jpg|400px]] <br /> | |
| − | + | <br /> | |
| − | + | ||
| − | + | ||
| − | [[Datei: | + | |
<br /> | <br /> | ||
| − | --[[Benutzer:Adores|Adores]] 14: | + | --[[Benutzer:Adores|Adores]] 14:58, 26. Nov. 2011 (CET) |
Aktuelle Version vom 27. November 2011, 17:29 Uhr
Hier findet ihr alle Aufgaben und Lösungen/Lösungsversuche:
Inhaltsverzeichnis |
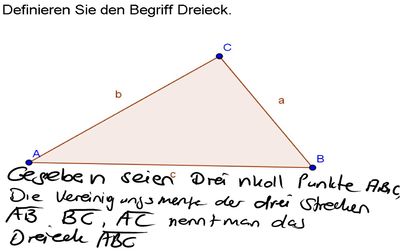
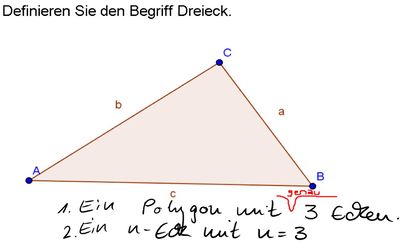
Aufgabe 1: Definition Dreieck
Definition 1
Definition 2
Aufgabe 2: Addition zweier Strecken (
+ 
=)
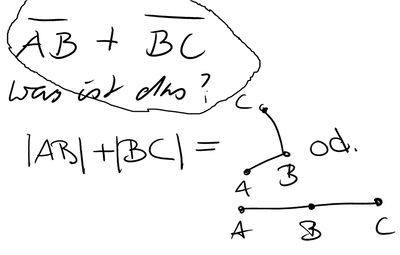
--> Wenn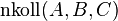 
, dann ist es nur die Summe der zwei Strecken.
--> Der Betrag der Strecke + der Betrag der Strecke ergibt wenn A,B und C drei kollineare Punkte der Betrag der Strecke 
.
Aufgabe 3: Definition Viereck (ohne Verwendung des Oberbegriffs n-Eck
Definition 1
--> Lösung nur bedingt richtig, je 3 von 4 Punkten müssten nicht kollinear sein (siehe Schaubild)
Definition 2
--> korrekte Lösung
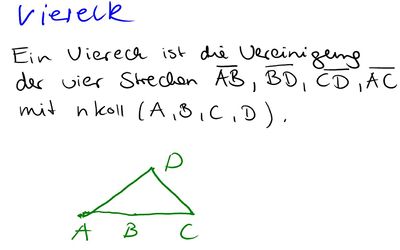
Aufgabe 4: Definition Viereck (mit Hilfe von Dreiecken)
Definition 1
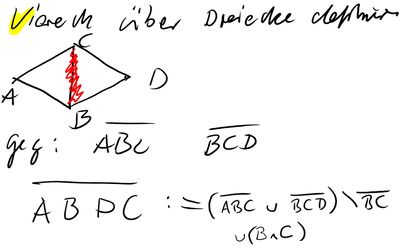
--> hier ist zu beachten, dass man B und C wieder aufführen muss, da sie aufgrund der Entfernung der Strecke wegfallen.
Definition 2
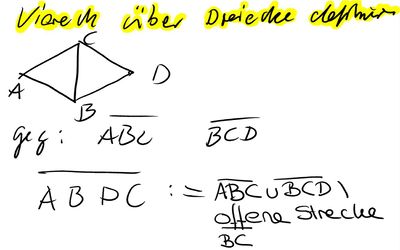
--> die oben genannte Problematik entfällt, wenn man die offene Strecke verwendet, da in dieser die Punkte B und C nicht enthalten sind.
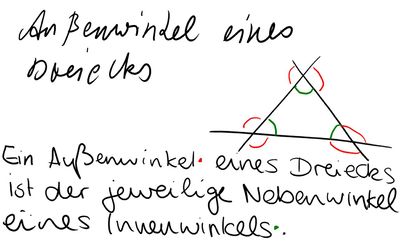
Aufgabe 5: Definition Außenwinkel eines Dreiecks
Definition 1
-->intuitive Definition, da anliegen kein mathematisch korrekter Ausdruck ist.
Definition 2
Aufgabe 6: Beweis Zwischenrelation: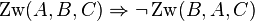 
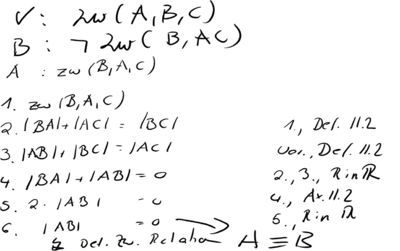
--Adores 14:58, 26. Nov. 2011 (CET)
