Übung Aufgaben 4 (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 4.4)
 
(10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
=Aufgaben zum Abstand=
+
== Aufgabe 4 ==
 +
Beweisen Sie mit Hilfe einer Wahrheitstabelle:<br /><br />
  
−
==Aufgabe 4.1==
+
<math>(\ A \Rightarrow B)  \wedge (\ B \Rightarrow A)  \Leftrightarrow (\ A \Leftrightarrow B) </math><br />
−
<u>'''Satz:'''</u>
+
−
::Von drei paarweise verschiedenen Punkten <math>\ A, B</math> und <math>\ C</math> ein und derselben Geraden <math>\ g</math> liegt genau einer zwischen den beiden anderen.
+
−
Beweisen Sie diesen Satz.
+
  
−
<br />
+
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br />
−
[[Lösung von Aufgabe 4.1 (SoSe_12)]]
+
[[Lösung von Zusatzaufgabe 2.4 (SoSe_12)]]
  
−
==Aufgabe 4.2==
+
== Aufgabe 5 ==  
−
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
+
Vergleichen Sie die Wahrheitswerte von<br />
−
<math>\operatorname Zw (A, B, C) </math> <math>\Rightarrow </math> <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
+
  
−
[[Tipps zu Aufgabe 4.2 (SoSe_12)]]
+
<math>(\ A \Rightarrow B) </math> und <math>(\ A  \wedge \neg B)</math>.<br />
−
<br /><br />
+
−
[[Lösung von Aufgabe 4.2 (SoSe_12)]]
+
  
−
==Aufgabe 4.3==
+
Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.<br />
−
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
+
[[Lösung von Zusatzaufgabe 2.5 (SoSe_12)]]
−
Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math>
+
  
 +
=Aufgaben zur Inzidenz im Raum=
 +
 +
'''Die Inzidenzaxiome können für die Geometrie im Raum erweitert werden. Lesen Sie sich hier die [[Inzidenz im Raum SoSe_12)]] durch, Sie benötigen die Axiome und Definitionen für die folgenden Aufgaben.'''
 
<br />
 
<br />
  
−
==Aufgabe 4.4==
 
−
Beweisen Sie: Zu jeder Strecke <math>\overline{AB} </math> existiert genau eine Strecke <math>\overline{AC} </math> mit <math>\left| AB \right| = \frac{1}{4} \left| AC \right| </math> und <math>\overline{AB} </math> <math> \subset</math>  <math>\overline{AC} </math>
 
  
−
<br />
+
==Aufgabe 3.4==
−
[[Lösung von Aufgabe 4.3 (SoSe_12)]]
+
Beweisen Sie Satz I.6: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.
 +
 
 +
[[Lösung von Aufg. 3.4 (SoSe_12)]]
 +
 
 +
 
 +
== Aufgabe 3.5 ==
 +
<u>'''Satz:'''</u>
 +
:Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
 +
 
 +
# Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen ''komplanar'' und ''kollinear'' zu verwenden.
 +
# Formulieren Sie den Satz noch einmal, ohne ''wenn-dann'' zu gebrauchen.
 +
# Beweisen Sie den Satz. Hier ein Anfang für den Beweis:
 +
<u>'''Beweis'''</u>
 +
::Es seien <math>\ A, B, C</math> und <math>\ D</math> vier Punkte, die nicht komplanar sind.
 +
<u>'''zu zeigen'''</u>
 +
:: ...
 +
<u>'''Annahme:'''</u>
 +
::Es gibt drei Punkte von den vier Punkten <math>\ A, B, C, D</math>, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...
 +
 
 +
[[Lösung von Aufg. 3.5 (SoSe_12)]]
 +
 
 +
 
 +
 
 +
== Aufgabe 4.5 ==
 +
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 3.3 und 3.5).
 +
 
 +
[[Lösung von Aufg. 4.5 (SoSe_12)]]

Aktuelle Version vom 19. April 2012, 09:50 Uhr

Inhaltsverzeichnis

Aufgabe 4

Beweisen Sie mit Hilfe einer Wahrheitstabelle:

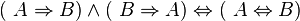
(\ A \Rightarrow B) \wedge (\ B \Rightarrow A) \Leftrightarrow (\ A \Leftrightarrow B)

Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Lösung von Zusatzaufgabe 2.4 (SoSe_12)

Aufgabe 5

Vergleichen Sie die Wahrheitswerte von

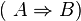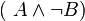(\ A \Rightarrow B) und (\ A \wedge \neg B).

Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
Lösung von Zusatzaufgabe 2.5 (SoSe_12)

Aufgaben zur Inzidenz im Raum

Die Inzidenzaxiome können für die Geometrie im Raum erweitert werden. Lesen Sie sich hier die Inzidenz im Raum SoSe_12) durch, Sie benötigen die Axiome und Definitionen für die folgenden Aufgaben.


Aufgabe 3.4

Beweisen Sie Satz I.6: Eine Ebene und eine nicht in ihr liegende Gerade haben höchstens einen Punkt gemeinsam.

Lösung von Aufg. 3.4 (SoSe_12)


Aufgabe 3.5

Satz:

Wenn vier Punkte nicht komplanar sind, sind je drei von ihnen nicht kollinear.
  1. Formulieren Sie den Satz noch einmal, ohne die Bezeichnungen komplanar und kollinear zu verwenden.
  2. Formulieren Sie den Satz noch einmal, ohne wenn-dann zu gebrauchen.
  3. Beweisen Sie den Satz. Hier ein Anfang für den Beweis:

Beweis

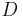Es seien \ A, B, C und \ D vier Punkte, die nicht komplanar sind.

zu zeigen

...

Annahme:

Es gibt drei Punkte von den vier Punkten \ A, B, C, D, die kollinear sind. Es mögen dieses o.B.d.A. die Punkte ...

Lösung von Aufg. 3.5 (SoSe_12)


Aufgabe 4.5

Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 3.3 und 3.5).

Lösung von Aufg. 4.5 (SoSe_12)

Von „http://geometrie.zum.de/index.php?title=Übung_Aufgaben_4_(SoSe_12)&oldid=11726“