Lösung von Aufgabe 2.7 S (SoSe 12): Unterschied zwischen den Versionen
(→Aufgabe 2.7) |
Oz44oz (Diskussion | Beiträge) (→Zu 4) |
||
| (13 dazwischenliegende Versionen von 6 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz.<br /> | Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz.<br /> | ||
| − | 1. Wenn ABCD vier rechte Innenwinkel hat, dann ist es ein Quadrat.<br /> | + | 1. Wenn <math>\overline {ABCD}</math> vier rechte Innenwinkel hat, dann ist es ein Quadrat.<br /> |
| − | 2. Wenn ein Punkt auf der Hypothenuse eines rechtwinkligen Dreiecks ABC liegt, dann ist es der Mittelpunkt des Umkreises des Dreiecks.<br /> | + | 2. Wenn ein Punkt auf der Hypothenuse eines rechtwinkligen Dreiecks <math>\overline {ABC}</math> liegt, dann ist es der Mittelpunkt des Umkreises des Dreiecks.<br /> |
3. Wenn sich die Diagonalen eines Vierecks schneiden, dann ist es konvex.<br /> | 3. Wenn sich die Diagonalen eines Vierecks schneiden, dann ist es konvex.<br /> | ||
| − | 4. Wenn die Symmetrieachsen von ABCD durch Geraden eindeutig bestimmt sind, dann liegen die Geraden auf den Diagonalen einer Raute.<br /> | + | 4. Wenn die Symmetrieachsen von <math>\overline {ABCD}</math> durch Geraden eindeutig bestimmt sind, dann liegen die Geraden auf den Diagonalen einer Raute.<br /> |
| − | 5. Wenn die Winkel SPQ und QRS konruent zueinander sind, dann ist PQRS ein Parallelogramm.<br /> | + | 5. Wenn die Winkel <math>\angle {SPQ}</math> und <math>\angle {QRS}</math> konruent zueinander sind, dann ist <math>\overline {PQRS}</math> ein Parallelogramm.<br /> |
| − | 6. Wenn die Innenwinkelsumme von ABC 180° beträgt, dann ist es ein Dreieck.<br /> | + | 6. Wenn die Innenwinkelsumme von <math>\overline {ABC}</math> 180° beträgt, dann ist es ein Dreieck.<br /> |
| + | |||
| + | |||
| + | |||
| + | == Zu 1 == | ||
| + | |||
| + | == Zu 2 == | ||
| + | |||
| + | Implikation: Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks. | ||
| + | |||
| + | Umkehrung: Die Hypotenuse eines rechtwinkligen Dreiecks ist der Durchmesser vom Umkreis dieses Dreiecks.--[[Benutzer:Oz44oz|Oz44oz]] 00:44, 1. Mai 2012 (CEST) | ||
| + | |||
| + | == Zu 3 == | ||
| + | |||
| + | == Zu 4 == | ||
| + | |||
| + | Implikation: Wenn ein Viereck eine Raute ist, dann sind beide Diagonalen Symmetrieachsen. | ||
| + | |||
| + | Umkehrung: Wenn beide Diagonalen eines Vierecks Symmetrieachsen sind, dann ist das Viereck eine Raute. (nicht wahr)--[[Benutzer:Oz44oz|Oz44oz]] 22:50, 1. Mai 2012 (CEST) | ||
| + | |||
| + | == Zu 5 == | ||
| + | |||
| + | Implikation : Wenn ein Viereck ein Paralellogramm ist, dann sind die gegenüberliegenden Winkel gleich groß. | ||
| + | |||
| + | Umkehrung: Wenn in einem Viereck die gegenüberliegenden Winkel gleich groß sind, dann ist das Viereck ein Paralellogramm . (nicht wahr; siehe Viereck, Quadrat)--[[Benutzer:Oz44oz|Oz44oz]] 22:50, 1. Mai 2012 (CEST) | ||
| + | |||
| + | == Zu 6 == | ||
| + | |||
| + | Implikation: Wenn das Vieleck ein Dreieck ist, dann beträgt die Innenwinkelsumme 180. | ||
| + | |||
| + | Umkehrung: Wenn in einem Vieleck die Innenwinkelsumme 180 beträgt, dann ist es ein Dreieck. ( wahr ) | ||
| + | |||
| + | Äquivalenz: Ein Vieleck ist genau dann ein Dreieck, wenn die Innenwinkelsumme 180 beträgt.--[[Benutzer:Oz44oz|Oz44oz]] 22:54, 1. Mai 2012 (CEST) | ||
| + | |||
| + | |||
Passende Äquivalenz bei:<br /> | Passende Äquivalenz bei:<br /> | ||
| − | 3. Die Diagonalen eines Vierecks schneiden sich | + | 3. Die Diagonalen eines Vierecks schneiden sich genau dann, wenn es konvex ist.<br /> |
| − | 6. ABC ist ein Dreieck, | + | 6. <math>\overline {ABC}</math> ist genau dann ein Dreieck, wenn seine Innenwinkelsumme 180° beträgt.<br /> |
| + | |||
| + | |||
| + | 2. Wenn der Mittelpunkt des Umkreises eines Dreiecks auf dessen Hypothenuse liegt, dann ist es ein rechtwinkliges Dreieck.--[[Benutzer:Goliath|Goliath]] 13:49, 29. Apr. 2012 (CEST) | ||
| + | |||
| + | 4. Wenn die Geraden Symmetrieachsen der Raute <math>\overline {ABCD}</math> sind, dann werden sie durch die Diagonalen der Raute eindeutig bestimmt.--[[Benutzer:Goliath|Goliath]] 13:49, 29. Apr. 2012 (CEST) | ||
| + | |||
| + | ===Kommentar M.G.=== | ||
| + | Die Schreibweise <math>\overline {ABC}</math> steht für ein Dreieck. Ich formuliere mal "Wenn die Innenwinkelsumme von <math>\overline {ABC}</math> 180° beträgt, dann ist es ein Dreieck." nur mit anderen Worten: Wenn die Innenwinkelsumme des Dreiecks <math>\overline{ABC}</math> 180° beträgt, dann ist <math>\overline{ABC}</math> ein Dreieck. Wieder so ein Fall von "Wenn du kein iPhone hast ... ."--[[Benutzer:*m.g.*|*m.g.*]] 17:55, 29. Apr. 2012 (CEST) | ||
| + | Ein passender Oberbegriff von Dreieck kann hilfreich sein.--[[Benutzer:*m.g.*|*m.g.*]] 17:57, 29. Apr. 2012 (CEST) | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
| + | |||
| + | Wenn ABC n=3, dann beträgt die Innenwinkelsumme 180 Grad. KeinKurpfälzer und --[[Benutzer:Wurzel|H2O]] 17:22, 30. Apr. 2012 (CEST) | ||
Aktuelle Version vom 1. Mai 2012, 22:58 Uhr
Inhaltsverzeichnis[Verbergen] |
Aufgabe 2.7
Bilden Sie die Umkehrungen der Implikationen aus Aufgabe 2.6. Formulieren Sie in den Fällen in denen es sinnvoll ist, Implikation und Umkehrung als Äquivalenz.
1. Wenn 
vier rechte Innenwinkel hat, dann ist es ein Quadrat.
2. Wenn ein Punkt auf der Hypothenuse eines rechtwinkligen Dreiecks 
liegt, dann ist es der Mittelpunkt des Umkreises des Dreiecks.
3. Wenn sich die Diagonalen eines Vierecks schneiden, dann ist es konvex.
4. Wenn die Symmetrieachsen von durch Geraden eindeutig bestimmt sind, dann liegen die Geraden auf den Diagonalen einer Raute.
5. Wenn die Winkel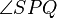 
und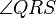 
konruent zueinander sind, dann ist 
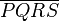ein Parallelogramm.
6. Wenn die Innenwinkelsumme von 180° beträgt, dann ist es ein Dreieck.
Zu 1
Zu 2
Implikation: Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks.
Umkehrung: Die Hypotenuse eines rechtwinkligen Dreiecks ist der Durchmesser vom Umkreis dieses Dreiecks.--Oz44oz 00:44, 1. Mai 2012 (CEST)
Zu 3
Zu 4
Implikation: Wenn ein Viereck eine Raute ist, dann sind beide Diagonalen Symmetrieachsen.
Umkehrung: Wenn beide Diagonalen eines Vierecks Symmetrieachsen sind, dann ist das Viereck eine Raute. (nicht wahr)--Oz44oz 22:50, 1. Mai 2012 (CEST)
Zu 5
Implikation : Wenn ein Viereck ein Paralellogramm ist, dann sind die gegenüberliegenden Winkel gleich groß.
Umkehrung: Wenn in einem Viereck die gegenüberliegenden Winkel gleich groß sind, dann ist das Viereck ein Paralellogramm . (nicht wahr; siehe Viereck, Quadrat)--Oz44oz 22:50, 1. Mai 2012 (CEST)
Zu 6
Implikation: Wenn das Vieleck ein Dreieck ist, dann beträgt die Innenwinkelsumme 180.
Umkehrung: Wenn in einem Vieleck die Innenwinkelsumme 180 beträgt, dann ist es ein Dreieck. ( wahr )
Äquivalenz: Ein Vieleck ist genau dann ein Dreieck, wenn die Innenwinkelsumme 180 beträgt.--Oz44oz 22:54, 1. Mai 2012 (CEST)
Passende Äquivalenz bei:
3. Die Diagonalen eines Vierecks schneiden sich genau dann, wenn es konvex ist.
6. ist genau dann ein Dreieck, wenn seine Innenwinkelsumme 180° beträgt.
2. Wenn der Mittelpunkt des Umkreises eines Dreiecks auf dessen Hypothenuse liegt, dann ist es ein rechtwinkliges Dreieck.--Goliath 13:49, 29. Apr. 2012 (CEST)
4. Wenn die Geraden Symmetrieachsen der Raute sind, dann werden sie durch die Diagonalen der Raute eindeutig bestimmt.--Goliath 13:49, 29. Apr. 2012 (CEST)
Kommentar M.G.
Die Schreibweise steht für ein Dreieck. Ich formuliere mal "Wenn die Innenwinkelsumme von 180° beträgt, dann ist es ein Dreieck." nur mit anderen Worten: Wenn die Innenwinkelsumme des Dreiecks 180° beträgt, dann ist ein Dreieck. Wieder so ein Fall von "Wenn du kein iPhone hast ... ."--*m.g.* 17:55, 29. Apr. 2012 (CEST)
Ein passender Oberbegriff von Dreieck kann hilfreich sein.--*m.g.* 17:57, 29. Apr. 2012 (CEST)
Wenn ABC n=3, dann beträgt die Innenwinkelsumme 180 Grad. KeinKurpfälzer und --H2O 17:22, 30. Apr. 2012 (CEST)
