Lösung von Aufgabe 4.1P (SoSe 12): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?<br /> *Parallelität von Geraden der Ebe…“) |
|||
| (3 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?<br /> | Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?<br /> | ||
| − | *Parallelität von Geraden der Ebene | + | *Parallelität von Geraden der Ebene<br /> |
| − | *Kongruenz geometrischer Figuren | + | Reflexivität: ja<br /> |
| − | *Teilbarkeit in <math>\mathbb{N}</math> | + | Symmetrie: ja<br /> |
| − | *Kleinerrelation in <math>\mathbb{R}</math> | + | Transitivität: ja<br /> |
| − | *Größer-Gleich-Relation in <math>\mathbb{R}</math> | + | äquiv.-rel.<br /> |
| − | *Ungleichheit in <math>\mathbb{R}</math> | + | *Kongruenz geometrischer Figuren<br /> |
| + | Reflexivität: ja<br /> | ||
| + | Symmetrie: ja<br /> | ||
| + | Transitivität: ja<br /> | ||
| + | äquiv.-rel.<br /> | ||
| + | *Teilbarkeit in <math>\mathbb{N}</math><br /> | ||
| + | Reflexivität: ja<br /> | ||
| + | Symmetrie: nö<br /> | ||
| + | Transitivität: ja<br /> | ||
| + | *Kleinerrelation in <math>\mathbb{R}</math><br /> | ||
| + | Reflexivität: nö <br /> | ||
| + | Symmetrie: nö<br /> | ||
| + | Transitivität: ja<br /> | ||
| + | *Größer-Gleich-Relation in <math>\mathbb{R}</math><br /> | ||
| + | Reflexivität: ja<br /> | ||
| + | Symmetrie: nö<br /> | ||
| + | Transitivität: ja<br /> | ||
| + | *Ungleichheit in <math>\mathbb{R}</math><br /> | ||
| + | Reflexivität: nö<br /> | ||
| + | Symmetrie: ja<br /> | ||
| + | Transitivität: nö<br /> | ||
| + | --[[Benutzer:Studentin|Studentin]] 01:07, 9. Mai 2012 (CEST) | ||
| + | Habe alles genauso, fand die Ungleichheit am schwierigsten zu lösen --[[Benutzer:Honeydukes|Honeydukes]] 18:28, 12. Mai 2012 (CEST) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
| + | |||
| + | Warum ist die Größer-Gleich-Relation auch reflexiv. a>=a ? Es kann doch nur a=a sein das ist doch ein Unterschied oder? -- Steffem | ||
| + | <br />die frage, die man sich stellen muss, lautet: ist irgendeine zahl aus <math>\mathbb{R}</math> größer-gleich sich selbst? <br />die antwortet "ja", weil: 3<math>\geq</math>3, 1000<math>\geq</math>1000 und a<math>\geq</math>a<br />daher reflexiv--[[Benutzer:Studentin|Studentin]] 17:58, 14. Jul. 2012 (CEST) | ||
Aktuelle Version vom 14. Juli 2012, 16:58 Uhr
Entscheiden Sie für die folgenden Relationen, ob es sich um reflexive, symmetrische sowie transitive Relationen handelt?
- Parallelität von Geraden der Ebene
Reflexivität: ja
Symmetrie: ja
Transitivität: ja
äquiv.-rel.
- Kongruenz geometrischer Figuren
Reflexivität: ja
Symmetrie: ja
Transitivität: ja
äquiv.-rel.
- Teilbarkeit in

Reflexivität: ja
Symmetrie: nö
Transitivität: ja
- Kleinerrelation in

Reflexivität: nö
Symmetrie: nö
Transitivität: ja
- Größer-Gleich-Relation in

Reflexivität: ja
Symmetrie: nö
Transitivität: ja
- Ungleichheit in

Reflexivität: nö
Symmetrie: ja
Transitivität: nö
--Studentin 01:07, 9. Mai 2012 (CEST)
Habe alles genauso, fand die Ungleichheit am schwierigsten zu lösen --Honeydukes 18:28, 12. Mai 2012 (CEST)
Warum ist die Größer-Gleich-Relation auch reflexiv. a>=a ? Es kann doch nur a=a sein das ist doch ein Unterschied oder? -- Steffem
die frage, die man sich stellen muss, lautet: ist irgendeine zahl aus  größer-gleich sich selbst?
größer-gleich sich selbst?
die antwortet "ja", weil: 3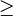 3, 1000
3, 1000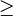 1000 und a
1000 und a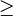 a
a
daher reflexiv--Studentin 17:58, 14. Jul. 2012 (CEST)

