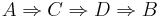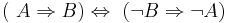Beweisen SoSe 12 S: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Erkennen Sie den Zusammenhang?) |
*m.g.* (Diskussion | Beiträge) (→Indirekter Beweis) |
||
| (16 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> | ||
| + | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- ---------------------------------------------------------------- ---> | ||
==Implikationen== | ==Implikationen== | ||
Aus der Schule kennen Sie bereits den so genannten ''Wechselwinkelsatz''. <br /> | Aus der Schule kennen Sie bereits den so genannten ''Wechselwinkelsatz''. <br /> | ||
| Zeile 48: | Zeile 52: | ||
{ Welche Aussagen sind wahr?} | { Welche Aussagen sind wahr?} | ||
| − | + Wenn ein Viereck zwei Paare paralleler Seiten hat, dann ist es ein Trapez. | + | + ''Wenn'' ein Viereck '''zwei Paare paralleler Seiten''' hat, ''dann'' ist es ein '''Trapez'''. |
| − | - Ein Viereck ist genau dann ein Trapez, wenn es zwei Paare paralleler Seiten hat. | + | - Ein Viereck ist ''genau dann'' ein '''Trapez''', ''wenn'' es '''zwei Paare paralleler Seiten''' hat. |
| − | + Wenn ein Viereck zwei Paare paralleler Seiten hat, dann ist es ein Parallelogramm. | + | + ''Wenn'' ein Viereck '''zwei Paare paralleler Seiten''' hat, ''dann'' ist es ein '''Parallelogramm'''. |
| − | + Ein Viereck ist genau dann ein Parallelogramm, wenn es zwei Paare paralleler Seiten hat. | + | + Ein Viereck ist'' genau dann'' ein '''Parallelogramm''', ''wenn'' es '''zwei Paare paralleler Seiten''' hat. |
| − | - Wenn ein Viereck zwei Paare paralleler Seiten hat, dann ist es ein Rechteck. | + | - ''Wenn'' ein Viereck '''zwei Paare paralleler Seiten''' hat, ''dann'' ist es ein '''Rechteck'''. |
| − | - Ein Viereck ist genau dann ein Rechteck, wenn es zwei Paare paralleler Seiten hat. | + | - Ein Viereck ist ''genau dann'' ein '''Rechteck''', ''wenn'' es '''zwei Paare paralleler Seiten''' hat. |
</quiz> | </quiz> | ||
| + | |||
==== Erkennen Sie den Zusammenhang?==== | ==== Erkennen Sie den Zusammenhang?==== | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 63: | Zeile 68: | ||
- ein Kriterium für die Behauptung. | - ein Kriterium für die Behauptung. | ||
</quiz> | </quiz> | ||
| + | ===Erklärung der Begriffe=== | ||
An dieser Stelle ist es sinnvoll, zwei wichtige Begriffe der mathematischen Logik einzuführen: '''hinreichende''' und '''notwendige Bedingung'''<br /> Lassen Sie uns die Begriffe an einem alltäglichen Beispiel erläutern:<br /> | An dieser Stelle ist es sinnvoll, zwei wichtige Begriffe der mathematischen Logik einzuführen: '''hinreichende''' und '''notwendige Bedingung'''<br /> Lassen Sie uns die Begriffe an einem alltäglichen Beispiel erläutern:<br /> | ||
Wir nehmen mal den folgenden Satz: Wenn die Deckenlampe leuchtet, dann ist das Zimmer hell. <br\> | Wir nehmen mal den folgenden Satz: Wenn die Deckenlampe leuchtet, dann ist das Zimmer hell. <br\> | ||
| Zeile 72: | Zeile 78: | ||
==Beweise== | ==Beweise== | ||
| + | ===Beispiel: Wir beweisen den Basiswinkelsatz=== | ||
| + | ====Der Satz==== | ||
| + | <u>Satz: (Basiswinkelsatz)</u> | ||
| + | :::Es sei <math>\overline{ABC}</math> ein Dreieck mit den schulüblichen Bezeichnungen (s. Skizze). | ||
| + | :::: Wenn <math>a \tilde= b</math>, dann <math>\alpha \tilde= \beta</math>. | ||
| + | ====Direkter Beweis==== | ||
| + | Voraussetzung: <math>a \tilde= b</math><br /> | ||
| + | Behauptung: <math>\alpha \tilde= \beta</math><br /> | ||
| + | Beweis:<br /> | ||
| + | Hilfskonstruktion: Es sei <math>M</math> der Mittelpunkt der Seite <math>\overline{AB}=c</math>. (Die Existenz dieses Punktes ist gesichert.) Wegen seiner Eigenschaft, der Mittelpunkt von <math>\overline{AB}</math> zu sein, hat der Punkt <math>M</math> zu den Endpunkten der Strecke <math>\overline{AB}</math> ein und denselben Abstand: | ||
| + | <math>|AM|=|BM|</math> bzw. <math>\overline{AM} \tilde= \overline{BM}</math>. | ||
| + | Weil die Strecke <math>\overline{MC}</math> wie jede Strecke zu sich selbst kongruent ist und die Seiten <math>a</math> und <math>b</math> nach Vorausetzung zueinander kongruent sind, sind nun die Teildreiecke <math>\overline{AMC}</math> und <math>\overline{BMC}</math> nach SSS zueinander kongruent. Aus dieser Dreieckskongruenz folgt die Kongruenz der Winkel <math>\alpha</math> und <math>\beta</math>. | ||
| + | |||
| + | q.e.d. | ||
| + | ====Indirekter Beweis==== | ||
| + | Wir schicken zunächst den folgenden bekannten Satz voraus: | ||
| + | Satz (*): In jedem Dreieck liegt dem größeren Winkel auch die größere Seite gegenüber. | ||
| + | Voraussetzung: <math>a \tilde= b</math><br /> | ||
| + | Behauptung: <math>\alpha \tilde= \beta</math><br /> | ||
| + | Zum Beweis der Behauptung nehmen wir an, dass unter der Voraussetzung <math>a \tilde= b</math><br /> die Negation der Behauptung gilt.<br /> | ||
| + | Annahme: <math>\alpha \not{\tilde=} \beta</math><br /> | ||
| + | Wenn die Winkel <math>\alpha</math> und <math>\beta</math> nicht kongruent sind, dann ist entweder der Winkel <math>\alpha</math> größer als der Winkel <math>\beta</math> oder umgekehrt der Winkel <math>\beta</math> größer als der Winkel <math>\alpha</math>. Sollte <math>|\alpha| > |\beta|</math> gelten, dann wäre nach (*) die Seite <math>a</math> länger als die Seite <math>b</math>. Wäre <math>|\beta| > |\alpha|</math>, dann müsste wiederum nach (*) die Seite <math>b</math> länger als die Seite <math>a</math> sein. Beides wäre ein Widerspruch zu unserer Voraussetzung <math>|a|=|b|</math>. Unsere Annahme ist somit zu verwerfen. | ||
| + | |||
| + | ===Ein wenig Theorie zum Beweisen=== | ||
Mathematische Sätze lassen sich im Unterschied zu Definitionen beweisen. Um einen Satz zu beweisen können verschiedene Beweistechniken angewendet werden.<br />Grundsätzlich unterscheidet man '''direkte''' von '''indirekten Beweisen'''. Außerdem gibt es noch so genannte '''Induktionsbeweise''' (vollständige Induktion, Wohlordnungsprinzip).<br /><br /> | Mathematische Sätze lassen sich im Unterschied zu Definitionen beweisen. Um einen Satz zu beweisen können verschiedene Beweistechniken angewendet werden.<br />Grundsätzlich unterscheidet man '''direkte''' von '''indirekten Beweisen'''. Außerdem gibt es noch so genannte '''Induktionsbeweise''' (vollständige Induktion, Wohlordnungsprinzip).<br /><br /> | ||
'''Direkter Beweis'''<br /> | '''Direkter Beweis'''<br /> | ||
| Zeile 84: | Zeile 114: | ||
<br /> | <br /> | ||
| + | <!--- ------------------------------------------------------------- ---> | ||
| + | |} | ||
| + | </div> | ||
[[Category:Geometrie_S]] | [[Category:Geometrie_S]] | ||
Aktuelle Version vom 4. Mai 2012, 13:41 Uhr
ImplikationenAus der Schule kennen Sie bereits den so genannten Wechselwinkelsatz. Notwenig, hinreichend, notwendig und hinreichendAufgaben zum EinstiegZwei Paare paralleler Seiten sind notwendig, hinreichend, notwendig und hinreichend für .. ?
Das Ganze noch mal in Wenn ... Dann ...
Erkennen Sie den Zusammenhang?Erklärung der BegriffeAn dieser Stelle ist es sinnvoll, zwei wichtige Begriffe der mathematischen Logik einzuführen: hinreichende und notwendige Bedingung BeweiseBeispiel: Wir beweisen den BasiswinkelsatzDer SatzSatz: (Basiswinkelsatz)
Direkter BeweisVoraussetzung: q.e.d. Indirekter BeweisWir schicken zunächst den folgenden bekannten Satz voraus:
Satz (*): In jedem Dreieck liegt dem größeren Winkel auch die größere Seite gegenüber.
Voraussetzung: Ein wenig Theorie zum BeweisenMathematische Sätze lassen sich im Unterschied zu Definitionen beweisen. Um einen Satz zu beweisen können verschiedene Beweistechniken angewendet werden.
Aufgabe:
Formulieren Sie die Kontraposition des Wechselwinkelsatzes. |
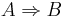
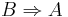
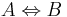
 Behauptung (Das Zimmer ist hell).
Behauptung (Das Zimmer ist hell). ein Dreieck mit den schulüblichen Bezeichnungen (s. Skizze).
ein Dreieck mit den schulüblichen Bezeichnungen (s. Skizze).
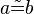 , dann
, dann 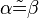 .
.
 der Mittelpunkt der Seite
der Mittelpunkt der Seite 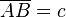 . (Die Existenz dieses Punktes ist gesichert.) Wegen seiner Eigenschaft, der Mittelpunkt von
. (Die Existenz dieses Punktes ist gesichert.) Wegen seiner Eigenschaft, der Mittelpunkt von  zu sein, hat der Punkt
zu sein, hat der Punkt 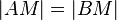 bzw.
bzw. 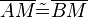 .
Weil die Strecke
.
Weil die Strecke 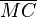 wie jede Strecke zu sich selbst kongruent ist und die Seiten
wie jede Strecke zu sich selbst kongruent ist und die Seiten  und
und  nach Vorausetzung zueinander kongruent sind, sind nun die Teildreiecke
nach Vorausetzung zueinander kongruent sind, sind nun die Teildreiecke 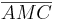 und
und 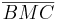 nach SSS zueinander kongruent. Aus dieser Dreieckskongruenz folgt die Kongruenz der Winkel
nach SSS zueinander kongruent. Aus dieser Dreieckskongruenz folgt die Kongruenz der Winkel  und
und  .
.
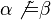
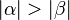 gelten, dann wäre nach (*) die Seite
gelten, dann wäre nach (*) die Seite 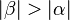 , dann müsste wiederum nach (*) die Seite
, dann müsste wiederum nach (*) die Seite 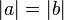 . Unsere Annahme ist somit zu verwerfen.
. Unsere Annahme ist somit zu verwerfen.