Streckenatragen oder das Axiom vom Lineal: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: == Fehlt noch was?== Wir wissen nun, dass eine Strecke <math>\overline{AB}</math> die Menge aller Punkte, die zwischen <math>\ A</math> und <math>\ B</math> liegen vere...)
 
(→‎Definition III.1: (Mittelpunkt einer Strecke))
 
(6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
== Fehlt noch was?==
+
== Der Mittelpunkt einer Strecke==
−
Wir wissen nun, dass eine Strecke <math>\overline{AB}</math> die Menge aller Punkte, die zwischen <math>\ A</math> und <math>\ B</math> liegen vereinigt mit der menge der beiden Endpunkte <math>\ A</math> und <math>\ B</math> ist. Zu unseren grundlegenden Vorstellungen von Strecken gehört, dass jede Strecke <math>\overline{AB}</math> einen Mittelpunkt <math>\ M</math> hat. <math>\ M</math> wäre der Punkt auf <math>\overline{AB}</math>, der sowohl zu <math>\ A</math> als auch zu <math>\ B</math> denselben Abstand <math>\frac{| \overline{AB} |}{2}</math> hat.
+
Wir wissen nun, dass eine offene Strecke <math>\overline{AB}</math> die Menge aller Punkte ist, die zwischen <math>\ A</math> und <math>\ B</math> liegen. Vereinigt man diese Menge mit der Menge der beiden Endpunkte <math>\ A</math> und <math>\ B</math>, so hat man die gesamte Strecke <math>\overline{AB}</math>. Zu unseren grundlegenden Vorstellungen von Strecken gehört, dass jede Strecke <math>\overline{AB}</math> einen Mittelpunkt <math>\ M</math> hat. <math>\ M</math> wäre der Punkt auf <math>\overline{AB}</math>, der sowohl zu <math>\ A</math> als auch zu <math>\ B</math> denselben Abstand <math>\frac{| \overline{AB} |}{2}</math> hat.
 +
 
 +
===== Definition III.1: (Mittelpunkt einer Strecke) =====
 +
::Wenn der Punkt <math>\ M</math> der Strecke <math>\overline{AB}</math> zu den Endpunkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand hat, so heißt er Mittelpunkt der Strecke <math>\overline{AB}</math>.

Aktuelle Version vom 31. Mai 2010, 10:54 Uhr

Der Mittelpunkt einer Strecke

Wir wissen nun, dass eine offene Strecke \overline{AB} die Menge aller Punkte ist, die zwischen \ A und \ B liegen. Vereinigt man diese Menge mit der Menge der beiden Endpunkte \ A und \ B, so hat man die gesamte Strecke \overline{AB}. Zu unseren grundlegenden Vorstellungen von Strecken gehört, dass jede Strecke \overline{AB} einen Mittelpunkt \ M hat. 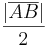\ M wäre der Punkt auf \overline{AB}, der sowohl zu \ A als auch zu \ B denselben Abstand \frac{| \overline{AB} |}{2} hat.

Definition III.1: (Mittelpunkt einer Strecke)
Wenn der Punkt \ M der Strecke \overline{AB} zu den Endpunkten \ A und \ B ein und denselben Abstand hat, so heißt er Mittelpunkt der Strecke \overline{AB}.
Von „http://geometrie.zum.de/index.php?title=Streckenatragen_oder_das_Axiom_vom_Lineal&oldid=1332“