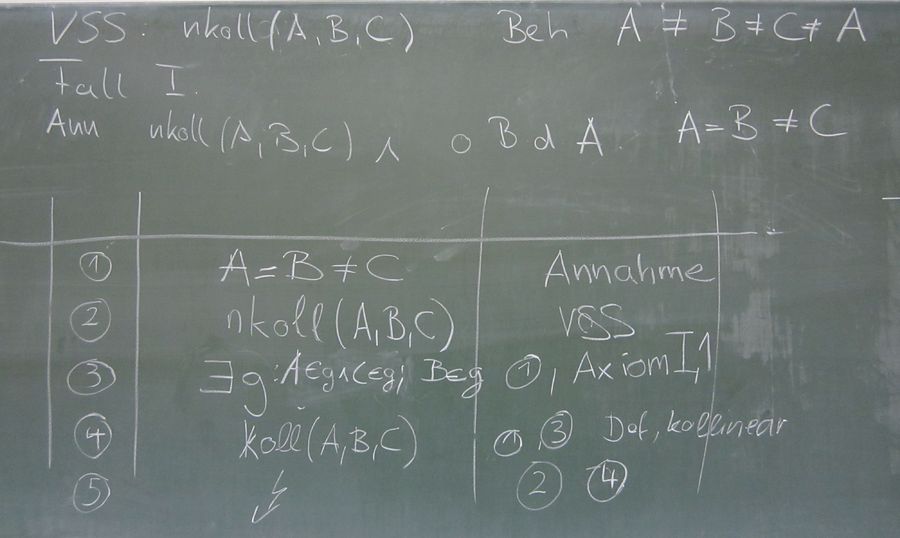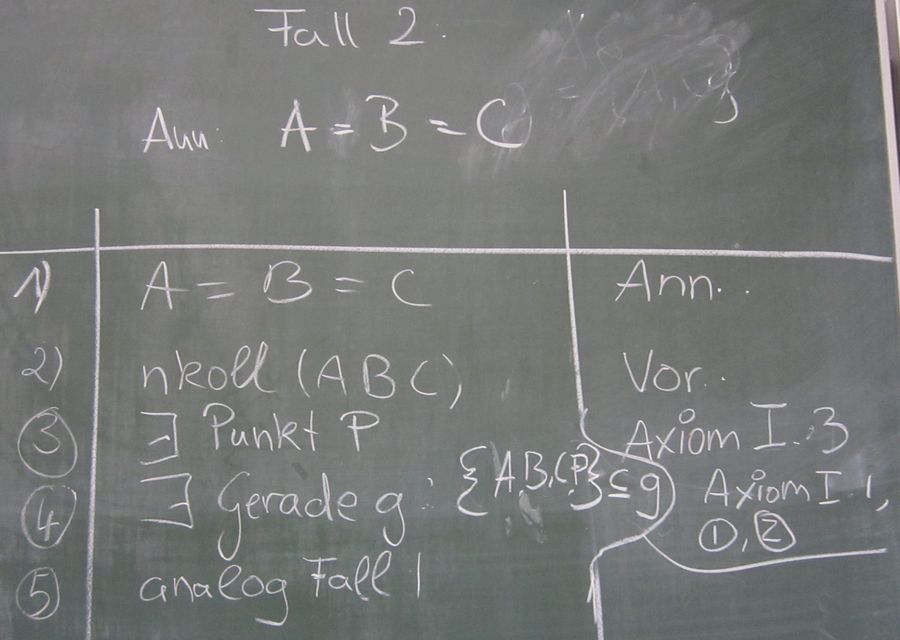Beweisidee Aufgabe 4.3.2 S Übung Heckl (SoSe2012): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
HecklF (Diskussion | Beiträge) |
HecklF (Diskussion | Beiträge) (→Fall 2: Annahme: Gelte A = B = C = A) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
dann kann nämlich Axiom I.1 nicht angewendet werden - diesen Fall schließen wir somit aus und unser Axiom kann angewendet werden,<br /> | dann kann nämlich Axiom I.1 nicht angewendet werden - diesen Fall schließen wir somit aus und unser Axiom kann angewendet werden,<br /> | ||
weil wir zwei verschiedene Punkte haben! --[[Benutzer:HecklF|Flo60]] 20:33, 16. Mai 2012 (CEST) | weil wir zwei verschiedene Punkte haben! --[[Benutzer:HecklF|Flo60]] 20:33, 16. Mai 2012 (CEST) | ||
| + | |||
| + | |||
| + | Woher nehmen wir die Berechtigung für Schritt (3), dass es einen weiteren Punkt gibt, der nicht A ist? Da steht etwas von Axiom I.3. Ich kann den Zusammenhang aber leider nicht verstehen. | ||
| + | <br /><br /> | ||
| + | Servus Junghansl,<br /> | ||
| + | Axiom I.3 lautet wie folgt: | ||
| + | |||
| + | Es gibt wenigstens 3 paarweise verschiedene Punkte, die nicht kollinear sind. | ||
| + | |||
| + | Da unsere Punkte A, B, C laut Voraussetzung nicht paarweise verschieden sind, existieren noch wenigstens zwei weitere Punkte D und P für die gilt, dass <math>D \neq P</math> ist und sie eben nicht identisch sind mit A, B und C. Aus diesem Grunde können wir uns ruhig einen von diesen beiden 'gönnen' :-). Ich hoffe, dass ich ein wenig helfen konnte. --[[Benutzer:HecklF|Flo60]] 21:10, 21. Mai 2012 (CEST) | ||
=Zurück zur Übungsseite= | =Zurück zur Übungsseite= | ||
Aktuelle Version vom 21. Mai 2012, 20:11 Uhr
Inhaltsverzeichnis |
Aufgabe 4.3
Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.
- Wir formulieren Satz I neu und beginnen mit „Es seien
 ,
,  und
und  drei Punkte.“ Ergänzen Sie: „Wenn
drei Punkte.“ Ergänzen Sie: „Wenn  ,
, und
und  nicht kollinear sind , dann sind sie paarweise verschieden .“
nicht kollinear sind , dann sind sie paarweise verschieden .“
- Beweisen Sie Satz I indirekt mit Widerspruch.
Beweis in zwei Fällen (Reihenfolge der Fälle ist irrelevant) durch Widerspruch:
Fall 1: Annahme: Gelte o. B. d. A. A = B  C
C
Fall 2: Annahme: Gelte A = B = C = A
Kommentar zu Fall 2:
Sinnvollerweise schreiben wir zu 3):, ansonsten könnte es ja sein, dass P = A ist;
dann kann nämlich Axiom I.1 nicht angewendet werden - diesen Fall schließen wir somit aus und unser Axiom kann angewendet werden,
weil wir zwei verschiedene Punkte haben! --Flo60 20:33, 16. Mai 2012 (CEST)
Woher nehmen wir die Berechtigung für Schritt (3), dass es einen weiteren Punkt gibt, der nicht A ist? Da steht etwas von Axiom I.3. Ich kann den Zusammenhang aber leider nicht verstehen.
Servus Junghansl,
Axiom I.3 lautet wie folgt:
Es gibt wenigstens 3 paarweise verschiedene Punkte, die nicht kollinear sind.
Da unsere Punkte A, B, C laut Voraussetzung nicht paarweise verschieden sind, existieren noch wenigstens zwei weitere Punkte D und P für die gilt, dass 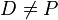 ist und sie eben nicht identisch sind mit A, B und C. Aus diesem Grunde können wir uns ruhig einen von diesen beiden 'gönnen' :-). Ich hoffe, dass ich ein wenig helfen konnte. --Flo60 21:10, 21. Mai 2012 (CEST)
ist und sie eben nicht identisch sind mit A, B und C. Aus diesem Grunde können wir uns ruhig einen von diesen beiden 'gönnen' :-). Ich hoffe, dass ich ein wenig helfen konnte. --Flo60 21:10, 21. Mai 2012 (CEST)