Lösung von Zusatzaufgabe 3.2 P (SoSe 12): Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
| − | Wäre es möglich, die Lösung zu dieser Teilaufgabe preiszugeben? Ich komme nämlich nicht weiter. | + | Wäre es möglich, die Lösung zu dieser Teilaufgabe preiszugeben? Ich komme nämlich nicht weiter.<br /><br /> |
| − | + | <span style="color: green">Sie sind eigentlich schon am Ziel, denn Sie haben gezeigt, dass <math>\neg(\ A \wedge \neg B)</math> äquivalent zu <math>(\ A \Rightarrow B) </math> ist. Jetzt müssten Sie das ganze nur noch richtig interpretieren, Stichwort: Widerspruchsbeweis.--[[Benutzer:Schnirch|Schnirch]] 15:06, 21. Mai 2012 (CEST)</span><br /> | |
| + | oben hat ein namenloser um die lösung gebeten, da hatte ich mein bild unten eingefügt.<br /> | ||
| + | ich verstehe nicht ganz, was bei der lösung noch fehlt?<br /> | ||
| + | ich habe gezeigt, dass beide aussagen das genaue gegenteil aussagen, sich also widersprechen.<br /> | ||
| + | reicht das nicht zu sehen, dass wenn <math>(\ A \Rightarrow B) </math> genau widersprüchlich zu <math>(A \wedge \neg B) </math> ist,<br /> dass dann <math>(\ A \Rightarrow B) </math> äquivalent zu <math>\neg(A \wedge \neg B) </math> ist? --[[Benutzer:Studentin|Studentin]] 17:08, 27. Mai 2012 (CEST)<br /><br /><br /> | ||
hier meine lösung: | hier meine lösung: | ||
| − | [[Datei:Zusatz_3.2p_001.jpg| | + | [[Datei:Zusatz_3.2p_001.jpg|600px]]--[[Benutzer:Studentin|Studentin]] 14:42, 21. Mai 2012 (CEST) |
Aktuelle Version vom 27. Mai 2012, 16:08 Uhr
Vergleichen Sie die Wahrheitswerte von
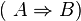und 
.
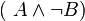Erklären Sie den Zusammenhang zwischen Ihrer Wahrheitstabelle und dem indirekten Beweis durch Widerspruch.
Lösung von Zusatzaufgabe 3.2_P (SoSe_12)
Wäre es möglich, die Lösung zu dieser Teilaufgabe preiszugeben? Ich komme nämlich nicht weiter.
Sie sind eigentlich schon am Ziel, denn Sie haben gezeigt, dass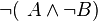 
äquivalent zu 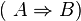ist. Jetzt müssten Sie das ganze nur noch richtig interpretieren, Stichwort: Widerspruchsbeweis.--Schnirch 15:06, 21. Mai 2012 (CEST)
oben hat ein namenloser um die lösung gebeten, da hatte ich mein bild unten eingefügt.
ich verstehe nicht ganz, was bei der lösung noch fehlt?
ich habe gezeigt, dass beide aussagen das genaue gegenteil aussagen, sich also widersprechen.
reicht das nicht zu sehen, dass wenn 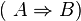genau widersprüchlich zu 
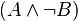ist,
dass dann 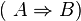äquivalent zu 
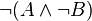ist? --Studentin 17:08, 27. Mai 2012 (CEST)
hier meine lösung:
--Studentin 14:42, 21. Mai 2012 (CEST)
