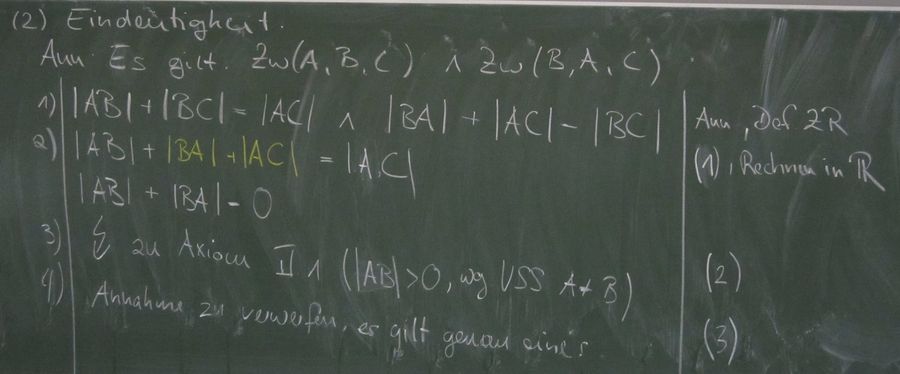Lösungsideen Übung Heckl 23.05.2012: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „==Aufgabe 5.1== <u>'''Satz:'''</u> ::Von drei paarweise verschiedenen Punkten <math>\ A, B</math> und <math>\ C</math> ein und derselben Geraden <math>\ g</math> …“)
 
(→‎Platz für Kommentare zu Aufgabe 5.2)
 
(8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 6: Zeile 6:
 
[[Datei: 23052012_5_1_1.JPG |900px]]
 
[[Datei: 23052012_5_1_1.JPG |900px]]
 
<br />
 
<br />
−
Die Behauptung wurde auf zwei verschiedene Arten und Weisen formuliert!
+
Die Behauptung wurde auf zwei verschiedene Arten und Weisen formuliert!
 
<br /><br />
 
<br /><br />
 
[[Datei: 23052012_5_1_2.JPG | 900px]]
 
[[Datei: 23052012_5_1_2.JPG | 900px]]
 
<br />
 
<br />
−
Diese gelben 'Häckchen' sind in Wirklichkeit keine 'Häckchen', sondern bedeuten das aussagelogische ODER (<math>\vee</math>)
+
Diese gelben 'Häckchen' sind in Wirklichkeit keine 'Häckchen', sondern bedeuten das aussagelogische ODER (<math>\vee</math>)
 
<br /><br />
 
<br /><br />
 
[[Datei: 23052012_5_1_3.JPG | 900px]]<br />
 
[[Datei: 23052012_5_1_3.JPG | 900px]]<br />
 
--[[Benutzer:HecklF|Flo60]] 21:29, 23. Mai 2012 (CEST)
 
--[[Benutzer:HecklF|Flo60]] 21:29, 23. Mai 2012 (CEST)
−
===Platz für Kommentare===
+
===Platz für Kommentare zu Aufgabe 5.1===
 
<br />
 
<br />
  
Zeile 20: Zeile 20:
  
 
<br />
 
<br />
 +
==Aufgabe 5.3==
 +
Zeigen Sie, dass für drei paarweise verschiedene Punkte <math>\ A, B</math> und <math>\ C</math> gilt:<br />
 +
Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math>
 +
<br /><br />
 +
[[Datei: 23052012_5_3_1.JPG | 900px]]
 +
<br /><br />
 +
Schritt III müsste eigentlich noch ergänzt werden mit der Begründung, warum nur <math>\operatorname(Zw) (A, B, C) \ oder \operatorname(Zw) (A, C, B) </math> <br />
 +
gelten kann (Definition Halbgerade; A ist Anfangspunkt).
 +
<br />
 +
[[Datei: 23052012_5_3_2.JPG | 900px]]
 +
<br /><br />--[[Benutzer:HecklF|Flo60]] 21:33, 23. Mai 2012 (CEST)
 +
 +
===Platz für Kommentare zu Aufgabe 5.2===
 +
<br />
 +
 +
Ich bin den Beweis noch einmal durchgegangen. Dabei sind mir 2 Dinge aufgefallen:
 +
<br />
 +
1. Müssten wir der Vollständigkeit halber bei Schritt 2 nicht auch koll(A,B,C) sagen?
 +
<br />
 +
Ja, da hast du natürlich recht. Es steckt zwar implizit in der Zwischenrelation drin - der besseren Übersicht <br />
 +
und tatsächlich der 'Vollständigkeit halber' macht es durchaus viel Sinn, das auzulagern. <br />
 +
Wir haben in diese Tabelle auch ziemlich viel (zu viel?) in der Begründungsspalte geparkt. <br />
 +
Es wäre sicherlich sinnvoll, die vielen Begründungen als Zwischenschritte auszulagern. <br />
 +
Wenn du magst - wäre sicherlich auch für die anderen hilfreich - kannst du den Teilbeweis nochmal extra in einer Tabelle <br />
 +
hier im Wiki ausformulieren.
 +
2. Fehlt uns nicht ein Schritt zwischen (2) und (3), nämlich /AB/ + /BC/ = /AC/, /AC/ + /CB/ = /AB/ mit der Begründung Ax. II.2 und (2)? Denn nur daraus können wir jetzt mit der Def. Zw den Schritt (3) herleiten (Oder?)
 +
Auch hier zeigt sich wieder der Nachteil, dass wir so gut wie alles, was wir zu bieten hatten in die Begründung <br />
 +
gestopft haben. Implizit steckt das schon drin (nämlich bei <math>C \neq B</math> und <math>|CB|>0 \ nach \ Axiom \ II.1</math>. <br />
 +
Du kannst das aber (und auch das scheint sinnvoller zu sein) auch als extrigen Schritt auslagern. Nur würde ich es nicht <br />
 +
ganz so aufwendig machen. Wenn man nach Schritt eins (und vllt. den ein oder anderen Zwischenschritt) sauber ausformuliert, <br />
 +
dass  <math>|CB|>0 \ nach \ Axiom \ II.1</math> gilt und <br />
 +
daraus dann (vllt. erneut in einem extra Schritt) nun eben der Widerspruch zur Annahme vorhanden ist, <br />
 +
dann brauchst du die Zwischenrelation ja auch gar nicht mehr als Begründung. Den Widerspruch erzeugen wir über <math>C \neq  B</math><br />
 +
Ich denke tatsächlich es ist wenn du kurz deine Beweisidee hier einbaust - ist ja nicht lange - und dann lässt sich besser <br />
 +
darüber reden.<br />
 +
Ich hoff aber, dass ich zumindest weiterhelfen konnte. Grundsätzlich sind deine Einwände absolut berechtigt und zeugen <br />
 +
von Verständnis für die Thematik - wir/ich habe/n in der Übung wohl unsauber gearbeitet :D. --[[Benutzer:HecklF|Flo60]] 23:05, 3. Jun. 2012 (CEST)
 +
 +
<br />
 +
 +
== Aufgabe 5.5 ==
 +
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).<br /><br />
 +
===Ein bereitgestelltes Skript einer Übungsteilnehmerin - dankeschön===
 +
[[Datei: 5_5_s_1.JPG | 900px]]
 +
<br /><br />
 +
[[Datei: 5_5_s_2.JPG | 900px]]
 +
<br /><br />
 +
 +
===Aus der Übung===
 +
[[Datei: 23052012_5_5.JPG | 900px]]
 +
<br /><br /><br />
 +
[[Datei: 23052012_5_5_z.JPG | 900px]]
 +
<br />--[[Benutzer:HecklF|Flo60]] 21:45, 23. Mai 2012 (CEST)
 +
 +
===Platz für Kommentare zu Aufgabe 5.5===
 +
<br />
 +
 +
 +
 +
 +
<br />
 +
 +
=Zurück zur Übungsseite=
 +
[[Übung Aufgaben 5 S (SoSe 12)]]
 +
 +
[[Kategorie: Einführung_S]] [[Kategorie: WIKI-Übung-Heckl]]

Aktuelle Version vom 3. Juni 2012, 22:13 Uhr

Inhaltsverzeichnis

Aufgabe 5.1

Satz:

Von drei paarweise verschiedenen Punkten \ A, B und \ C ein und derselben Geraden \ g liegt genau einer zwischen den beiden anderen.



23052012 5 1 1.JPG 

Die Behauptung wurde auf zwei verschiedene Arten und Weisen formuliert!



23052012 5 1 2.JPG 

Diese gelben 'Häckchen' sind in Wirklichkeit keine 'Häckchen', sondern bedeuten das aussagelogische ODER (\vee)



23052012 5 1 3.JPG
--Flo60 21:29, 23. Mai 2012 (CEST)

Platz für Kommentare zu Aufgabe 5.1




Aufgabe 5.3

Zeigen Sie, dass für drei paarweise verschiedene Punkte \ A, B und \ C gilt:
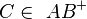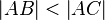Wenn C \in \ AB^{+} und \left| AB \right| < \left| AC \right| dann gilt \operatorname Zw (A, B, C)

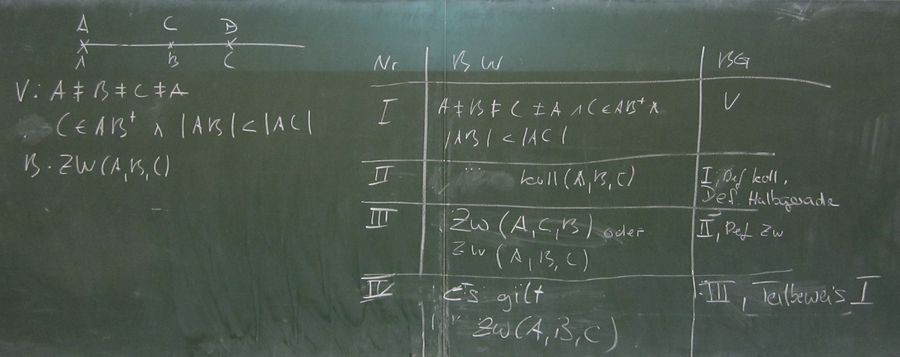
23052012 5 3 1.JPG 

Schritt III müsste eigentlich noch ergänzt werden mit der Begründung, warum nur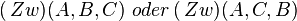 \operatorname(Zw) (A, B, C) \ oder \operatorname(Zw) (A, C, B)  

gelten kann (Definition Halbgerade; A ist Anfangspunkt).


23052012 5 3 2.JPG

--Flo60 21:33, 23. Mai 2012 (CEST)

Platz für Kommentare zu Aufgabe 5.2


Ich bin den Beweis noch einmal durchgegangen. Dabei sind mir 2 Dinge aufgefallen:
1. Müssten wir der Vollständigkeit halber bei Schritt 2 nicht auch koll(A,B,C) sagen? 

Ja, da hast du natürlich recht. Es steckt zwar implizit in der Zwischenrelation drin - der besseren Übersicht 

und tatsächlich der 'Vollständigkeit halber' macht es durchaus viel Sinn, das auzulagern. 

Wir haben in diese Tabelle auch ziemlich viel (zu viel?) in der Begründungsspalte geparkt. 

Es wäre sicherlich sinnvoll, die vielen Begründungen als Zwischenschritte auszulagern. 

Wenn du magst - wäre sicherlich auch für die anderen hilfreich - kannst du den Teilbeweis nochmal extra in einer Tabelle 

hier im Wiki ausformulieren.

2. Fehlt uns nicht ein Schritt zwischen (2) und (3), nämlich /AB/ + /BC/ = /AC/, /AC/ + /CB/ = /AB/ mit der Begründung Ax. II.2 und (2)? Denn nur daraus können wir jetzt mit der Def. Zw den Schritt (3) herleiten (Oder?) 

Auch hier zeigt sich wieder der Nachteil, dass wir so gut wie alles, was wir zu bieten hatten in die Begründung 

gestopft haben. Implizit steckt das schon drin (nämlich bei C \neq B und |CB|>0 \ nach \ Axiom \ II.1. 

Du kannst das aber (und auch das scheint sinnvoller zu sein) auch als extrigen Schritt auslagern. Nur würde ich es nicht 

ganz so aufwendig machen. Wenn man nach Schritt eins (und vllt. den ein oder anderen Zwischenschritt) sauber ausformuliert, 
 
dass  |CB|>0 \ nach \ Axiom \ II.1 gilt und 

daraus dann (vllt. erneut in einem extra Schritt) nun eben der Widerspruch zur Annahme vorhanden ist, 

dann brauchst du die Zwischenrelation ja auch gar nicht mehr als Begründung. Den Widerspruch erzeugen wir über C \neq  B

Ich denke tatsächlich es ist wenn du kurz deine Beweisidee hier einbaust - ist ja nicht lange - und dann lässt sich besser 

darüber reden.

Ich hoff aber, dass ich zumindest weiterhelfen konnte. Grundsätzlich sind deine Einwände absolut berechtigt und zeugen 

von Verständnis für die Thematik - wir/ich habe/n in der Übung wohl unsauber gearbeitet :D. --Flo60 23:05, 3. Jun. 2012 (CEST)


Aufgabe 5.5

Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung die Sätze aus Aufgabe 4.3 und Zusatzaufgabe 4.4).

Ein bereitgestelltes Skript einer Übungsteilnehmerin - dankeschön

5 5 s 1.JPG

5 5 s 2.JPG

Aus der Übung

23052012 5 5.JPG


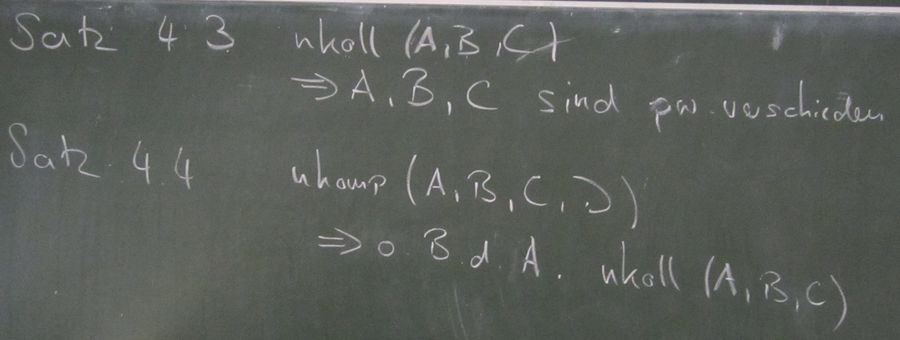
23052012 5 5 z.JPG
--Flo60 21:45, 23. Mai 2012 (CEST)

Platz für Kommentare zu Aufgabe 5.5





Zurück zur Übungsseite

Übung Aufgaben 5 S (SoSe 12)

Von „http://geometrie.zum.de/index.php?title=Lösungsideen_Übung_Heckl_23.05.2012&oldid=14187“