Jede Abbildung ist durch drei nichtkollineare Punkte und deren Bilder eindeutig bestimmt - eine Diskussion: Unterschied zwischen den Versionen
HecklF (Diskussion | Beiträge) (→Was gibt es denn zu diskutieren?) |
(→{{Schrift_orange|Diskussion II - völlig anderes Thema: 'Schwarze Löcher im Raum?'}}) |
||
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | =Vorbemerkung= | + | ={{Schrift_orange|Diskussion I}}= |
| + | ==Vorbemerkung== | ||
Rein aus Erfahrung zeigt sich (leider), dass sich wohl auch in diese Diskussion nur wenige, bis gar keine Studis einbringen. Daher mein Appell: Einbringen :-) - nur so zum Spass um auch mal über andere Dinge zu diskutieren! | Rein aus Erfahrung zeigt sich (leider), dass sich wohl auch in diese Diskussion nur wenige, bis gar keine Studis einbringen. Daher mein Appell: Einbringen :-) - nur so zum Spass um auch mal über andere Dinge zu diskutieren! | ||
| − | =Was gibt es denn zu diskutieren?= | + | ==Was gibt es denn zu diskutieren?== |
Wir haben zur Erarbeitung des Reduktionssatzes die Gültigkeit des folgenden Satzes gezeigt: | Wir haben zur Erarbeitung des Reduktionssatzes die Gültigkeit des folgenden Satzes gezeigt: | ||
| Zeile 26: | Zeile 27: | ||
==Beweis zur Zentrischen Streckung (ZS-Beweis)== | ==Beweis zur Zentrischen Streckung (ZS-Beweis)== | ||
| + | ===Vorüberlegung:=== | ||
| + | Ganz offensichtlich wird dieser Beweis derart ablaufen, dass das Streckzentrum durch zwei sich schneidende Geraden ermittelt wird. Benötigen wir also noch drei Punkte oder reichen zwei und deren Bilder? | ||
| + | Für den Fall, dass wir lediglich zwei Punkte A und B und deren Bilder A' und B' betrachten, kann es sein, dass gilt: koll(Z, A, B). Der Beweis wäre dann nicht durchführbar! Wir brauchen also drei nichtkollineare Punkte und deren Bilder. | ||
| + | ===Beweis=== | ||
| + | Ebene Geometrie. Seien A, B und C drei nichtkollineare Punkte und A', B', C' deren Bilder bei der zentrischen Streckung <math>ZS_Z,_k</math> mit dem Streckzentrum Z und dem Streckfaktor k. Behauptung: Für alle Punkte der Ebene ist die Abbildung eindeutig bestimmt. | ||
| + | Beweis erneut durch Widerspruch; Annahme: Es existiert ein Punkt D mit <math>ZS_Z,_k(D)</math> = D' und D* und D' <math>\neq</math> D*.<br /><br /> | ||
| + | |||
| + | {| class="wikitable sortable" | ||
| + | !Überschrift 1!!Überschrift 2 | ||
| + | |- | ||
| + | | 1 || Es existieren die Geraden AA', BB' und CC' || Inzidenzaxiom I.1 :-) | ||
| + | |- | ||
| + | | 2 || Wegen nkoll(A, B, C) schneiden sich wenigstens zwei dieser Geraden im Punkt Z || Definition zentrische Streckung, Voraussetzung, (1) | ||
| + | |- | ||
| + | | 3 || Nach Definition zentrischer Streckung gilt: koll(Z, D, D', D*) || (2), Indidenzaxiom I.1 (Z und D liegen auf einer Gerade) | ||
| + | |- | ||
| + | | 4 || k = <math>\frac{|ZA'|} {|ZA|} = \frac{|ZB'|} {|ZB|} = \frac{|ZC'|} {|ZC|}</math> || Voraussetzung, Definition zentrische Streckung | ||
| + | |- | ||
| + | | 5 || Es gilt: <math>|Z ZS_Z,_k(D)| = |ZD|*k </math>|| (4), Definition zentrische Streckung | ||
| + | |- | ||
| + | | 6 || Nach dem Axiom vom Lineal gibt es auf einem Strahl genau einen Punkt mit dem Abstand <math>|ZD|*k </math> - da wir unsere zentrische Streckung mit einem gerichteten Vektor definiert haben, kann es keine zwei Punkte auf einem Strahl geben für den dieser Abstand gilt. | ||
| + | |} | ||
| + | <br /> | ||
| + | Das geht wohl auch einfacher. Interessant vor allem der Aspekt, dass ich den gerichteten Vektor benötige. Hätten wir zentrische Streckung anders definiert, hätte ich ein Problem und könnte den Beweis gar nicht führen! --[[Benutzer:HecklF|Flo60]] 16:49, 26. Mai 2012 (CEST) | ||
| + | |||
| + | ={{Schrift_orange|Diskussion II - völlig anderes Thema: 'Schwarze Löcher im Raum?'}}= | ||
| + | Ganz offensichtlich gibt es Situationen, die das menschliche Hirn an den Rand seiner Kapazitätsgrenze bringen. Ein Beispiel dafür ist folgendes: Man nehme ein beliebiges Wort (Namen oder noch besser einen abstrakten Begriff, der nicht mit einem Gegenstand in Verbindung gebracht werden kann) und sage es solange vor sich hin, bis es jeglichen Sinn verliert und nur noch eine Aneinanderreihung von Buchstaben zu sein scheint :-).<br /> | ||
| + | Ein weiteres Beispiel ist die Frage, was denn hinter unserem Universum ist - nix kann es ja irgendwie nicht sein, denn das Universum muss ja irgendwo liegen<sup>1</sup>. Wahrscheinlich sucht hier die Religion nach Antworten - oder wenn man es mit Dan Brown hält (Autor 'Illuminati'), dann das 'Gottpartikel' oder die Wissenschaftler im CERN in der Schweiz. Appropos CERN: Vor nicht allzulanger Zeit gab es dort bedenken, dass durch die Partikelkollision im LEP (Large Electron-Positron Collider) zur Entstehung von schwarzen Löchern käme. Nun stellt sich folgende Frage: | ||
| + | |||
| + | <sup>1</sup> Nö, das Universum liegt nicht irgendwo, sondern es ist überall (nach Definition "Universum" bzw. "WeltALL(!)"). Wenn also Raum nur innerhalb des Universums existiert, dann kann nichts hinter dem Universum sein, denn "hinter" bezeichnet eine Raumlage-Beziehung. Jedweges Philosophieren über Dinge außerhalb unseres räumlich definierten Wahrnehmungsapparates kann also nur enden mit den Worten: "Kein Schimmer." oder mit Sokrates: "Ich weiß, dass ich nichts weiß.". |D [[Benutzer:Wexstabenverbuxler|Dr.plag.Schavan]] ([[Benutzer Diskussion:Wexstabenverbuxler|Diskussion]]) 13:56, 31. Jul. 2014 (CEST) | ||
| + | |||
| + | Können wir in unserer Mathematik auch ein schwarzes Loch schaffen - ohne CERN? | ||
| + | |||
| + | Ich denke, dass das möglich ist und zwar relativ einfach. Ich definiere Schwarzes Loch wie folgt: | ||
| + | |||
| + | Definition (Schwarzes Loch): Sei Z ein Punkt des Raums. Wenn Z Streckzentrum der zentrischen Streckung <math>ZS_Z_k</math> mit k = 0 ist, <br /> | ||
| + | dann ist Z schwarzes Loch des Raums. | ||
| + | |||
| + | {{Schrift_orange|Und jetzt sind wir wieder bei den Grenzen des menschlichen Hirns:}}<br /> | ||
| + | Wir haben natürlich bei unserer Zentrischen Streckung k <math>\neq</math> 0 definiert - aber warum sollten wir das nicht zulassen - es gibt ja schwarze Löcher auch in Wirklichkeit :-). Stellt sich allerdings wieder die alte Frage: Wenn alle Punkte des Raumes (ich habe deshalb den Raum und nicht die Ebene gewählt, weil es schöner ist :-) ) auf den Punkt Z abgebildet werden, was passiert dann mit dem Raum an sich? Er kann ja eigentlich nicht kleiner werden? Wer kennt die Antwort? Gibt es eine? | ||
| + | <br /> | ||
| + | --[[Benutzer:HecklF|Flo60]] 08:38, 29. Mai 2012 (CEST)<br /><br /> | ||
| + | '''42'''<br />;-) --[[Benutzer:Studentin|Studentin]] 23:23, 5. Jun. 2012 (CEST) | ||
| + | <br /><br /> | ||
| + | {{Schrift_grün|:D :D :D :D}} | ||
| + | <br /><br /> | ||
| + | Ich glaube aber, dass ich herausgefunden habe, wo das Eichhörnchen die Nuss vergraben hat: Aufgrund unserer Definition von Bewegung gilt, dass die Ebene auf sich abgebildet wird und Streckenlängen invariant sind. Jetzt haben wir es nur nicht mehr mit Bewegungen zu tun, aber immer noch mit einer Abbildung. D. h. dass unser Raum aus (doch relativ unspektakulären Gründen) erhalten bleibt und alle Punkte auf unser Z abgebildet werden - nichts desto trotz bleiben die Urbilder im Raum und demnach bleibt auch der Raum erhalten. Weil das aber langweilig ist, finde ich sollte man eine neue Geometrie erschaffen, in der Abbildungen wie folgt definiert werden: | ||
| + | |||
| + | {{Schrift_grün|<math>Definition_{Neue Geometrie} \ (Abbildung):</math>}} <br /> | ||
| + | Eine Menge von Punkten wird abgebildet,<br /> | ||
| + | wenn sie im Sinne der Euklid'schen Geometrie abgebildet werden mit der Ausnahme, <br /> | ||
| + | dass die Urbilder nach der jeweiligen Abbildung in Rauch aufgehen. | ||
| + | <br />--[[Benutzer:HecklF|Flo60]] 19:20, 7. Jun. 2012 (CEST) | ||
| + | |||
| + | =Zurück zur Übersichtsseite= | ||
| + | [[Das WIKI für die Veranstaltung Elementargeometrie]] | ||
| + | |||
| + | [[Kategorie:Elementargeometrie]] | ||
Aktuelle Version vom 31. Juli 2014, 12:56 Uhr
Inhaltsverzeichnis |
Diskussion I
Vorbemerkung
Rein aus Erfahrung zeigt sich (leider), dass sich wohl auch in diese Diskussion nur wenige, bis gar keine Studis einbringen. Daher mein Appell: Einbringen :-) - nur so zum Spass um auch mal über andere Dinge zu diskutieren!
Was gibt es denn zu diskutieren?
Wir haben zur Erarbeitung des Reduktionssatzes die Gültigkeit des folgenden Satzes gezeigt:
Jede Bewegung ist durch drei nichtkollineare Punkte und deren Bilder eindeutig bestimmt.
Nun stellt sich die Frage: Gilt das auch für Abbildungen allgemein?
Zunächst denke ich kann man das nicht pauschalisieren, denn eine Abbildung muss ja nur linkstotal und rechtseindeutig sein, d. h. wenn meine Abbildung derart bestimmt ist, dass ich drei Punkte A, B, C habe und diese nach gut dünken derart auf die Ebene 'regnen' lasse, dass jedes Urbild ein Bild hat, dann ist das auch eine (sehr willkürliche) Abbildung.
Für welche Abbildungen gilt es denn dann?
| Abbildung | Gültigkeit (ja/nein)? | Siehe Beweis |
|---|---|---|
| 'geregnete Abbildung' | Keine Gültigkeit | siehe Einleitung |
| Alle Bewegungen | Gültigkeit | siehe Folien Reduktionssatz |
| Alle NAF von Bewegungen | Gültigkeit | NAF von Bewegung ist auch Bewegung |
| zentrische Streckung | Gültigkeit | siehe ZS-Beweis unten |
| 5 | 5 | 5 |
Beweis zur Zentrischen Streckung (ZS-Beweis)
Vorüberlegung:
Ganz offensichtlich wird dieser Beweis derart ablaufen, dass das Streckzentrum durch zwei sich schneidende Geraden ermittelt wird. Benötigen wir also noch drei Punkte oder reichen zwei und deren Bilder? Für den Fall, dass wir lediglich zwei Punkte A und B und deren Bilder A' und B' betrachten, kann es sein, dass gilt: koll(Z, A, B). Der Beweis wäre dann nicht durchführbar! Wir brauchen also drei nichtkollineare Punkte und deren Bilder.
Beweis
Ebene Geometrie. Seien A, B und C drei nichtkollineare Punkte und A', B', C' deren Bilder bei der zentrischen Streckung 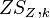 mit dem Streckzentrum Z und dem Streckfaktor k. Behauptung: Für alle Punkte der Ebene ist die Abbildung eindeutig bestimmt.
Beweis erneut durch Widerspruch; Annahme: Es existiert ein Punkt D mit
mit dem Streckzentrum Z und dem Streckfaktor k. Behauptung: Für alle Punkte der Ebene ist die Abbildung eindeutig bestimmt.
Beweis erneut durch Widerspruch; Annahme: Es existiert ein Punkt D mit 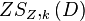 = D' und D* und D'
= D' und D* und D'  D*.
D*.
| Überschrift 1 | Überschrift 2 | |
|---|---|---|
| 1 | Es existieren die Geraden AA', BB' und CC' | Inzidenzaxiom I.1 :-) |
| 2 | Wegen nkoll(A, B, C) schneiden sich wenigstens zwei dieser Geraden im Punkt Z | Definition zentrische Streckung, Voraussetzung, (1) |
| 3 | Nach Definition zentrischer Streckung gilt: koll(Z, D, D', D*) | (2), Indidenzaxiom I.1 (Z und D liegen auf einer Gerade) |
| 4 | k =  |
Voraussetzung, Definition zentrische Streckung |
| 5 | Es gilt: 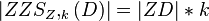 |
(4), Definition zentrische Streckung |
| 6 | Nach dem Axiom vom Lineal gibt es auf einem Strahl genau einen Punkt mit dem Abstand 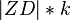 - da wir unsere zentrische Streckung mit einem gerichteten Vektor definiert haben, kann es keine zwei Punkte auf einem Strahl geben für den dieser Abstand gilt. - da wir unsere zentrische Streckung mit einem gerichteten Vektor definiert haben, kann es keine zwei Punkte auf einem Strahl geben für den dieser Abstand gilt.
|
Das geht wohl auch einfacher. Interessant vor allem der Aspekt, dass ich den gerichteten Vektor benötige. Hätten wir zentrische Streckung anders definiert, hätte ich ein Problem und könnte den Beweis gar nicht führen! --Flo60 16:49, 26. Mai 2012 (CEST)
Diskussion II - völlig anderes Thema: 'Schwarze Löcher im Raum?'
Ganz offensichtlich gibt es Situationen, die das menschliche Hirn an den Rand seiner Kapazitätsgrenze bringen. Ein Beispiel dafür ist folgendes: Man nehme ein beliebiges Wort (Namen oder noch besser einen abstrakten Begriff, der nicht mit einem Gegenstand in Verbindung gebracht werden kann) und sage es solange vor sich hin, bis es jeglichen Sinn verliert und nur noch eine Aneinanderreihung von Buchstaben zu sein scheint :-).
Ein weiteres Beispiel ist die Frage, was denn hinter unserem Universum ist - nix kann es ja irgendwie nicht sein, denn das Universum muss ja irgendwo liegen1. Wahrscheinlich sucht hier die Religion nach Antworten - oder wenn man es mit Dan Brown hält (Autor 'Illuminati'), dann das 'Gottpartikel' oder die Wissenschaftler im CERN in der Schweiz. Appropos CERN: Vor nicht allzulanger Zeit gab es dort bedenken, dass durch die Partikelkollision im LEP (Large Electron-Positron Collider) zur Entstehung von schwarzen Löchern käme. Nun stellt sich folgende Frage:
1 Nö, das Universum liegt nicht irgendwo, sondern es ist überall (nach Definition "Universum" bzw. "WeltALL(!)"). Wenn also Raum nur innerhalb des Universums existiert, dann kann nichts hinter dem Universum sein, denn "hinter" bezeichnet eine Raumlage-Beziehung. Jedweges Philosophieren über Dinge außerhalb unseres räumlich definierten Wahrnehmungsapparates kann also nur enden mit den Worten: "Kein Schimmer." oder mit Sokrates: "Ich weiß, dass ich nichts weiß.". |D Dr.plag.Schavan (Diskussion) 13:56, 31. Jul. 2014 (CEST)
Können wir in unserer Mathematik auch ein schwarzes Loch schaffen - ohne CERN?
Ich denke, dass das möglich ist und zwar relativ einfach. Ich definiere Schwarzes Loch wie folgt:
Definition (Schwarzes Loch): Sei Z ein Punkt des Raums. Wenn Z Streckzentrum der zentrischen Streckung Fehler beim Parsen(PNG-Konvertierung fehlgeschlagen. Bitte die korrekte Installation von LaTeX und dvipng überprüfen (oder dvips + gs + convert)): ZS_Z_k mit k = 0 ist,
dann ist Z schwarzes Loch des Raums.
Und jetzt sind wir wieder bei den Grenzen des menschlichen Hirns:
Wir haben natürlich bei unserer Zentrischen Streckung k  0 definiert - aber warum sollten wir das nicht zulassen - es gibt ja schwarze Löcher auch in Wirklichkeit :-). Stellt sich allerdings wieder die alte Frage: Wenn alle Punkte des Raumes (ich habe deshalb den Raum und nicht die Ebene gewählt, weil es schöner ist :-) ) auf den Punkt Z abgebildet werden, was passiert dann mit dem Raum an sich? Er kann ja eigentlich nicht kleiner werden? Wer kennt die Antwort? Gibt es eine?
0 definiert - aber warum sollten wir das nicht zulassen - es gibt ja schwarze Löcher auch in Wirklichkeit :-). Stellt sich allerdings wieder die alte Frage: Wenn alle Punkte des Raumes (ich habe deshalb den Raum und nicht die Ebene gewählt, weil es schöner ist :-) ) auf den Punkt Z abgebildet werden, was passiert dann mit dem Raum an sich? Er kann ja eigentlich nicht kleiner werden? Wer kennt die Antwort? Gibt es eine?
--Flo60 08:38, 29. Mai 2012 (CEST)
42
;-) --Studentin 23:23, 5. Jun. 2012 (CEST)
:D :D :D :D
Ich glaube aber, dass ich herausgefunden habe, wo das Eichhörnchen die Nuss vergraben hat: Aufgrund unserer Definition von Bewegung gilt, dass die Ebene auf sich abgebildet wird und Streckenlängen invariant sind. Jetzt haben wir es nur nicht mehr mit Bewegungen zu tun, aber immer noch mit einer Abbildung. D. h. dass unser Raum aus (doch relativ unspektakulären Gründen) erhalten bleibt und alle Punkte auf unser Z abgebildet werden - nichts desto trotz bleiben die Urbilder im Raum und demnach bleibt auch der Raum erhalten. Weil das aber langweilig ist, finde ich sollte man eine neue Geometrie erschaffen, in der Abbildungen wie folgt definiert werden:

Eine Menge von Punkten wird abgebildet,
wenn sie im Sinne der Euklid'schen Geometrie abgebildet werden mit der Ausnahme,
dass die Urbilder nach der jeweiligen Abbildung in Rauch aufgehen.
--Flo60 19:20, 7. Jun. 2012 (CEST)

